 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Частинні похідні та їх геометричний зміст
Нехай функція декількох змінних визначена в деякій відкритій області D.
Означення 1.12. Границю відношення частинного приросту функції по якомусь аргументу в точці  до приросту цього аргумента при останньому прямуючому до нуля в випадку існування та скінченності границі називають частинною похідною від розглядуваної функції по вказаному аргументу.
до приросту цього аргумента при останньому прямуючому до нуля в випадку існування та скінченності границі називають частинною похідною від розглядуваної функції по вказаному аргументу.
Для функції двох змінних частинну похідну по х позначають одним із символів
 ;
;  ;
; 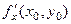 .
.
Аналогічно частинну похідну по у позначають відповідно
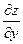 ;
;  ;
; 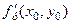 .
.
Отже, за означенням 1.12,частинні похідні 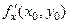 та
та 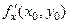 визначаються такими співвідношеннями:
визначаються такими співвідношеннями:
 ,
,
 .
.
Якщо замість фіксованої точки  беруть довільну точку
беруть довільну точку 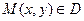 , то частинні похідні відповідно записують
, то частинні похідні відповідно записують 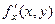 та
та  .
.
Операцію знаходження частинних похідних функції декількох змінних називають її диференціюванням.
Зауваження 1.7. Оскільки в означенні частинної похідної функції по якомусь з аргументів всі інші аргументи вважаються сталими, то при диференціюванні даної функції по цьому аргументу треба її диференціювати як функцію цієї однієї змінної, вважаючи решту змінних сталими. Тому правила знаходження частинних похідних функції декількох змінних ті самі, що й правила диференціювання функції однієї змінної.
Приклад 1.10. Знайти частинні похідні функцій:
а)  ; б)
; б)  .
.
Р о з в′ я з а н н я
а)  ,
,
 ;
;
б)  ;
;

 ;
;
 .
.
Зауваження 1.8. Як відомо, для функції однієї змінної неперервність її є необхідною умовою існування похідної в розглядуваній точці. Виявляється, що для функцій декількох змінних це не так. В цьому можна переконатись, розглянувши уже відому нам функцію

Для цієї функції її частинні прирости в точці О (0;0) дорівнюють:
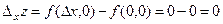 ;
; 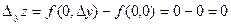 .
.
Тому існують
 ,
,
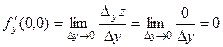 .
.
Але нам відомо (приклад 1.9), що дана функція в точці О(0;0) є розривна.
Відзначимо також, що із неперервності функції в точці ще не випливає існування її частинних похідних в цій точці. Дійсно, наприклад, функція  є визначена і неперервна в усіх точках площини, зокрема і в точці О(0;0), Але в цій точці не існує частинних похідних по жодному з аргументів.
є визначена і неперервна в усіх точках площини, зокрема і в точці О(0;0), Але в цій точці не існує частинних похідних по жодному з аргументів.
Висновок 1.1. Зі сказаного вище та зауваження 1.8 випливає, що ніякого зв¢язку між неперервністю функції декількох змінних в точці та існуванням її частинних похідних в цій точці немає.
 З¢ясуємо тепер геометричний зміст частинних похідних функції двох змінних.
З¢ясуємо тепер геометричний зміст частинних похідних функції двох змінних.
Нехай функція 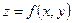 зображена поверхнею
зображена поверхнею 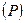 (рис. 1.5). В області D визначення функції візьмемо довільну точку
(рис. 1.5). В області D визначення функції візьмемо довільну точку  . Цій точці на поверхні
. Цій точці на поверхні  відповідає точка
відповідає точка  .
.
Враховуючи зауваження 1.7, при знаходженні частинної похідної по аргументу х функції 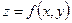 в точці
в точці  змінна у вважається сталою, яка дорівнює
змінна у вважається сталою, яка дорівнює 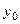 . Отже,функція
. Отже,функція  при
при  є функцією однієї змінної
є функцією однієї змінної 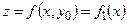 .
.
Геометричним образом цієї функції є лінія перетину поверхні  площиною
площиною
 . На рисунку 1.5 це лінія KN 0 L. Похідна
. На рисунку 1.5 це лінія KN 0 L. Похідна  функції
функції 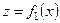 в точці
в точці  означає тангенс кута
означає тангенс кута  , який утворює дотична до кривої KN 0 L в точці N 0, з додатним напрямком осі Ox. Очевидно, що
, який утворює дотична до кривої KN 0 L в точці N 0, з додатним напрямком осі Ox. Очевидно, що  .
.
Отже, зі сказаного вище та з останньої рівності випливає такий геометричний зміст частинної похідної по х функції  : частинна похідна по х функції
: частинна похідна по х функції  в точці
в точці  дорівнює тангенсу кута між додатним напрямком осі Ох і дотичною, проведеною в точці
дорівнює тангенсу кута між додатним напрямком осі Ох і дотичною, проведеною в точці 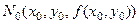 до кривої KN 0 L.
до кривої KN 0 L.
Якщо для функції  взяти
взяти  і провести міркування, аналогічні до вище проведених, то отримаємо наступний геометричний зміст частинної похідної по у функції
і провести міркування, аналогічні до вище проведених, то отримаємо наступний геометричний зміст частинної похідної по у функції  в точці
в точці  : частинна похідна по у функції
: частинна похідна по у функції  в точці
в точці  дорівнює тангенсу кута
дорівнює тангенсу кута  між додатним напрямком осі Оу і дотичною, проведеною в точці
між додатним напрямком осі Оу і дотичною, проведеною в точці 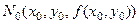 до кривої, яка утвориться при перетині поверхні
до кривої, яка утвориться при перетині поверхні  площиною, яка проходить через точку N 0 і паралельна площині yOz.
площиною, яка проходить через точку N 0 і паралельна площині yOz.
Лекція 2 Диференційованість функції декількох змінних
2.1 Означення диференційованості, зв¢язок з неперервністю та існуванням частинних похідних
Нехай функція двох змінних  визначена в деякій області D, для якої точка
визначена в деякій області D, для якої точка  є внутрішньою. Надамо аргументам х та у в даній точці приростів
є внутрішньою. Надамо аргументам х та у в даній точці приростів  та
та 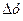 , одночасно не рівних нулю, так, щоб точка
, одночасно не рівних нулю, так, щоб точка  належала області D.
належала області D.
Означення 2.1. Функція  називається диференційованою в точці
називається диференційованою в точці  , якщо її повний приріст в цій точці можна подати у вигляді
, якщо її повний приріст в цій точці можна подати у вигляді
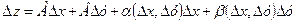 , (2.1)
, (2.1)
де А та В не залежать від приростів  та
та 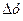 , а
, а  та
та  - нескінченно малі функції при
- нескінченно малі функції при  та
та  , тобто
, тобто
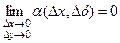 ,
,  . (2.2)
. (2.2)
Приклад 2.1. Для функції  повний приріст в довільній точці
повний приріст в довільній точці  можна записати так:
можна записати так:
 .
.
Легко бачити, що повний приріст для заданої функції записано в формі (2.1) з 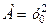 ,
,  ,
, 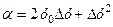 ,
,  , які задовольняють всім умовам в означенні 2.1. Отже, наша функція диференційована в усіх точках площини.
, які задовольняють всім умовам в означенні 2.1. Отже, наша функція диференційована в усіх точках площини.
Нижченаведені теореми стосуватимуться зв¢язкудиференційованості з неперервністю та існуванням частинних похідних.
Теорема 2.1. Якщо функція  диференційована в точці
диференційована в точці  , то вона неперервна в цій точці.
, то вона неперервна в цій точці.
Д о в е д е н н я. Згідно означення 2.1 для повного приросту функції  в точці
в точці  має місце рівність (2.1). Кожний з чотирьох доданків правої частини цієї рівності є нескінченно малою функцією при
має місце рівність (2.1). Кожний з чотирьох доданків правої частини цієї рівності є нескінченно малою функцією при  та
та  , значить, і їхня сума – нескінченно мала функція при
, значить, і їхня сума – нескінченно мала функція при  та
та  , тобто
, тобто
 .
.
Ця рівність означає неперервність нашої функції в точці М 0.
Теорему доведено.
Зауваження 2.1. Як випливає з цієї теореми, неперервність функції в точці є
необхідною умовою диференційованості в цій точці. Ми нижче переконаємось,
що неперервність не є достатньою умовою диференційованості.
Теорема 2.2. Якщо функція  диференційована в точці
диференційована в точці  , то в цій точці існують частинні похідні функції, причому
, то в цій точці існують частинні похідні функції, причому
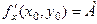 ,
,  . (2.3)
. (2.3)
Д о в е д е н н я. Для нашої функції в точці  виконується рівність (2.1). Покладемо в цій рівності
виконується рівність (2.1). Покладемо в цій рівності  , а
, а 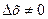 . Тоді повний приріст
. Тоді повний приріст  співпаде з частинним приростом
співпаде з частинним приростом 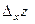 і рівність (2.1) набуде такого вигляду:
і рівність (2.1) набуде такого вигляду:
 .
.
Розділивши обидві частини останньої рівності на  , матимемо:
, матимемо:
 .
.
З врахуванням (2.2) ми бачимо, що існує  .
.
Але за означенням  . Це означає, що існує
. Це означає, що існує
 .
.
Якщо ж в рівності (2.1 покласти  , а
, а  , то отримаємо:
, то отримаємо:
 .
.
Розділивши обидві частини цієї рівності на 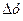 і перейшовши до границі при
і перейшовши до границі при  , дістанемо
, дістанемо
 .
.
Теорему доведено.
Зауваження 2.2. З останньої теореми випливає, що необхідною умовою диференційованості функції декількох змінних в точці є існування усіх частинних похідних в цій точці. Відзначимо, що для функції однієї змінної існування її похідної в точці є необхідною і достатньою умовою диференційованості функції в цій точці. Але для диференційованості функції декількох змінних в точці існування усіх її частинних похідних в цій точці не є достатньою умовою. Це випливає з наступних міркувань.
В зауваженні 1.8 ми вказали функцію

яка в точці О(0;0) має частинні похідні, але разом з тим розривна в цій точці, тому, відповідно до теореми 2.1, не може бути диференційованою в точці О(0;0).
Зауваження 2.3. Як видно з попередніх міркувань, ніякого зв¢язку між неперервністю функції декількох змінних в точці та існуванням частинних похідних в цій точці немає.
Теорема 2.3. Якщо функція  в околі точки
в околі точки  має частинні похідні і ці частинні похідні є неперервними функціями в точці
має частинні похідні і ці частинні похідні є неперервними функціями в точці  , то функція
, то функція  диференційована в даній точці.
диференційована в даній точці.
Д о в е д е н н я. Повний приріст функції в точці  можемо записати так:
можемо записати так:
 (2.4)
(2.4)
Вираз у перших дужках – приріст в точці х 0 функції однієї змінної  , а вираз в других дужках є приростом в точці у 0 функції однієї змінної
, а вираз в других дужках є приростом в точці у 0 функції однієї змінної 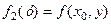 . Відповідно до умови теореми функції
. Відповідно до умови теореми функції 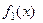 та
та  мають відповідно похідні (це частинні похідні від функції
мають відповідно похідні (це частинні похідні від функції 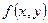 ) в деяких околах точок
) в деяких околах точок  та
та  . Тому за теоремою Лагранжа ці прирости можна записати так:
. Тому за теоремою Лагранжа ці прирости можна записати так:
 ,
,
 . (2.5)
. (2.5)
де  та
та  - якісь числа з інтервала (0;1).
- якісь числа з інтервала (0;1).
Розглянемо функції
 ,
,
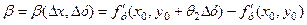 . (2.6)
. (2.6)
Оскільки обидві частинні похідні  та
та 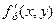 є неперервними функціями в точці
є неперервними функціями в точці  , то
, то
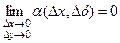 ,
,  .
.
Рівності (2.6) можемо переписати так:
 ,
,
 .
.
Тоді, з врахуванням (2.5), повний приріст (2.4) запишеться наступним чином:
 . (2.7)
. (2.7)
Значить, відповідно до означення 2.1, функція  диференційована в точці
диференційована в точці  .
.
Теорему доведено.
Поиск по сайту: