АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Алгоритм знаходження функції, оберненої до даної

Читайте также:
  1. XII. ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ
  2. Алгоритм
  3. Алгоритм MD4
  4. Алгоритм RC6
  5. Алгоритм RSA
  6. Алгоритм Брезенхема для окружности
  7. Алгоритм Брезенхема.
  8. Алгоритм взятия мазка из носа и зева.
  9. Алгоритм вибіркового методу
  10. Алгоритм вставки элемента в список после элемента с указанным ключом
  11. Алгоритм выполнения прически
  12. Алгоритм вычисления кодов Шеннона — Фано

1.Визначаємо, чи є задана функція, оборотна на всій області визначення. Якщо ні, виділяємо підмножину області визначення, де існує функція, обернена до даної.

2. Розв’язуємо рівняння відносно змінної х, тт. знаходимо функцію 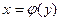, яка є обернена до даної.

3. Міняємо позначення змінних, незалежна-х; залежна-у.

 

2)Теорема: Графік функції , оберненої до функції f, симетричний графіку f відносно прямої у=х.

Доведення:

-оборотна. -обернена. Точка М(х;у) належить графіку f, а точка N(у;х)-графіку . Згадані точки симетричні відносно прямої у=х, отже і графіки оберненої та оборотної симетричні відносно прямої у=х.

 

Теорема: Якщо функція монотонна на проміжку, то вона на ньому оборотна. Обернена до неї функція визначена на області значень оборотної і також зберігає вид монотонності оборотної.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)