Перетворення тригонометричних виразів за допомогою введення допоміжного аргументу

Цей прийом полягає в тому, що де­яке число зображають як тригонометричну функцію відповідного ар­гументу φ, а потім для перетворення застосовують тригонометричні то­тожності.

Наприклад 1. Перетворити на добуток суму дійсних чисел А і В.

Розв’язання:

Нехай , тоді

.

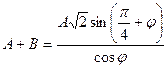, де .

Наприклад 2. Перетворити на добуток А=аsin α + bcos α, де а, b — дійсні числа, а b 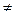0.

Розв'язання: .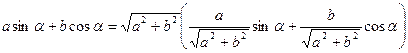

,

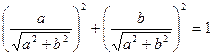то можна підібрати такий кут φ, щоб , .

.

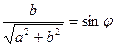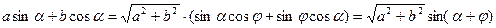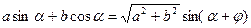,де кут φ визначають із системи:

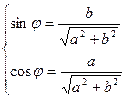
Лекція 8.

Тема: Обернені функції. Обернені тригонометричні функції та їх графіки.

План.

1) Поняття про обернену функцію.

2) Графік оберненої функції.

3) Функція, обернена до функції .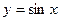

4) Функція, обернена до функції .

5) Функція, обернена до функції .

6) Функція, обернена до функції .

1) Поняття про обернену функцію.

Наприклад: У формулі 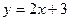виразити х через у.

Розв’язання:

Вираз виду 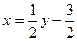- лінійна функція, обернена до функції 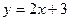, що називається оборотною. Переписавши вираз у звичних позначеннях, маємо .

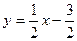У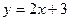

У=х

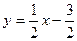
х

Графіки обох функцій симетричні відносно прямої у=х.

Необхідна і достатня умова оборотності: функція має набувати кожного свого значення лише для одного значення аргументу.

Достатня умова існування оберненої функції: монотонність на всій області визначення.

Оберненою до даної оборотної функції називається така функція 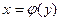, яка кожному у із множини значень функції ставить у відповідність єдине число х з області її визначення, тт. оборотна функція має обернену .

Поиск по сайту: