Обернені тригонометричні функції

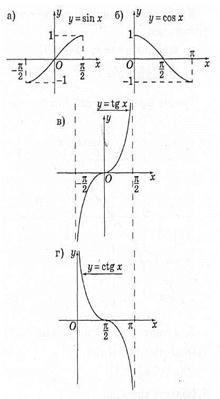
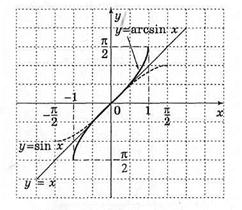
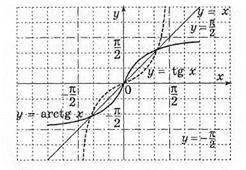
Розглянемо графіки тригономет­ричних функцій на одному з проміжків, де вони строго монотонні.

Мал. 14.

Отже, кожна з цих функцій на вказаних проміжках має обернену функцію.

3)Функція у = arcsin x (арксинус)

Оберненою тригонометричною функ­цією у=arcsin х називають величину (дуги, кута, числа) у, узяту в проміжку 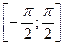, синус якої дорівнює х, тобто у=arcsin х, якщо sin у=х і .

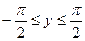З цього означення випливають такі тотожності:

.

.

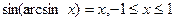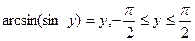Графік функції у=arcsin x:

Властивості функції у=arcsin x:

1. Область визначення:

D(y):X = R[-1;1].

2. Область значення:

.

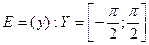Мал.15.

3.Нулі функції: х=0.

4.Парність і непарність:arcsin (-х)=arcsin х, функція непарна.

5. Проміжки знакосталості:

у > 0 для (0; 1]. у < 0 для [-1; 0).

6. Інтервали монотонності: у зростає від 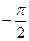до 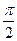на [-1;1].

7. Найбільше та найменше значення: найбільше значення 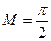функції при х=1;

найменше значення 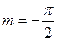функції при х=-1.

8. Інтервали опуклості: опукла вгору для (-1;0);опукла вниз для (0;1).

4)Функціяу = arccos x(арккосинус)

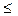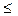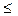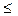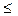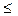Оберненою тригонометричною функцією у=arccosx називають величину (дуги, кута, числа) у, узяту з проміжку [0;π], синус якої дорівнює х, тобто у = arccosx, якщо cosу=х і 0 у π.З цього означення випливають такі тотожності: сos(arccos х)=х, -1 х 1. arccos(сos у)=у, 0 у π.

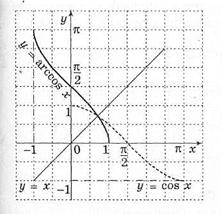
Графік функції у=arccos х:

Мал.16.

Властивості функції у = arccos x:

1. Область визначення:D(y):X = [-1;1].

2. Область значень:E(y):Y =[0; π].

3. Нулі функції: х = 1.

4. Парність і непарність:arccos(-x) =π arccos x, функція не є парною і не є непар­ною.

5.Проміжки знакосталості:у > 0 для всіх [-1; 1].

6.Інтервали монотонності: функція у = arccosx спадає від π до 0 на проміжку [-1; 1].

7.Найбільше та найменше значення: найбільше значення М = π при х = -1;

найменше значення m = 0 при х = 1

8. Інтервали опуклості: опукла вгору для (0; 1]; опукла вниз для [-1; 0).

5)Функція у= arctg х (арктангенс)

Оберненою тригонометричною функ­цією у=arctgх називають величину (дуги, кута, числа) у у проміжку 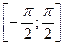, тангенс якої дорівнює х. Тобто у=arctg х, якщо tg у=х і 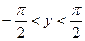.З цього означення випливають такі тотожності:

tg (arctg x)=х, R.arctg (tg y)=y, .

Графік функції у = arctg x:

Мал.17.

Властивості функції у = arctg x:

1. Область визначення:D(y):X=R.

2.Область значень: .

3.Нулі функції: х = 0.

4.Парність і непарність:arctg (-х)=-arctg x, функція непарна.

5.Проміжки знакосталості: у > 0, для 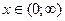.у < 0, для .

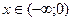6. Інтервали монотонності:функція у=arctgх зростає для всіх R.

7. Найбільше й найменше значення:
функція не має ні найменшого, ні найбільшого значення.

8. Інтервали опуклості:опукла вгору для 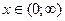.опукла вниз для .

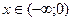6)Функція у = arcctg x (арккотангенс)

Оберненою тригонометричною функ­цією у=arcctg х називають величину (дуги, кута, числа) у, у проміжку (0;π) котангенс якої дорівнює х. Тобто у= arcctg х, якщо ctg y = x i y (0; π).З цього означення випливають такі тотожності:

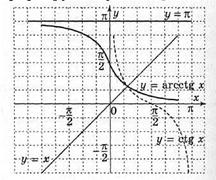
ctg(arcctg x)=x, x R.arcctg(ctg y)=y, 0<y<π.

Графік функції у=arcctg x:

Мал.18.

Властивості функції у=arcctg x:

1. Область визначення:D(y):X=R.

2.Область значень:E(y):Y =(0; π).

3. Нулі функції.Функція нулів не має.

4. Парність і непарність: arcctg(-х)=π-arcctg x,функція ні парна, ні непарна.

5. Проміжки знакосталості: у>0 для всіх .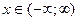

6. Інтервали монотонності: функція у=arcctg x строго спадає для всіх х R.

7. Найбільше та найменше значення:
функція не має ні найменшого, ні найбільшого значення.

8. Інтервали опуклості: опукла вгору для 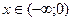; опукла вниз для .

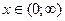Лекція 9.

Тема: Найпростіші тригонометричні рівняння.

План.

1. Рівняння виду

2. Рівняння виду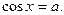

3. Рівняння виду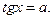

1.Рівняння виду

Якщо , то рівняння розв’язків не має.

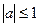Якщо , то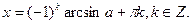

Особливі випадки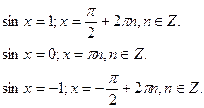

Зауваження: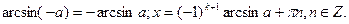

2.Рівняння виду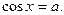

Якщо , то рівняння розв’язків не має.

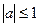Якщо , то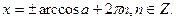

Особливі випадки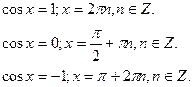

Зауваження: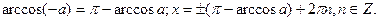

3.Рівняння виду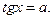

.

Зауваження: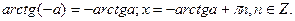

Лекція 10.

Тема: Основні способи розв’язування тригонометричних рівнянь.

План.

1. Рівняння, що зводяться до алгебраїчних за допомогою основних формул.

2. Рівняння, що зводяться до виду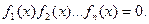

3. Однорідні.

4. Рівняння, що розв’язуються за формулами додавання та наслідками до них.

5. Рівняння виду .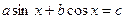

6. Рівняння, що розв’язуються перетворенням сум у добуток.

7. Рівняння, що розв’язуються перетворенням добутку двох тригонометричних функцій у суму.

8. Рівняння, що розв’язуються пониженням степеня.

9. Рівняння виду .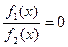

1.Рівняння, що зводяться до алгебраїчних за допомогою основних формул.

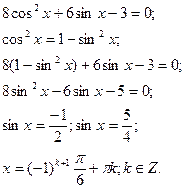
2.Рівняння, що зводяться до виду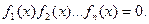

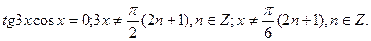
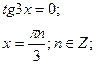
або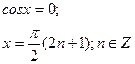

Не належить ОДЗ рівняння.

3.Однорідні.

А) 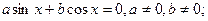однорідні І степеня відносно 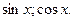Ділим обидві частини на .

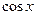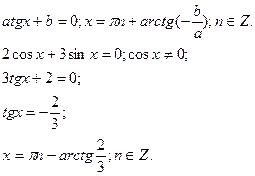
Б) 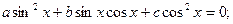однорідне ІІ степеня. Ділим на .

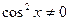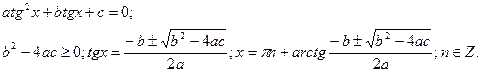
4.Рівняння, що розв’язуються за формулами додавання та наслідками до них.

Наприклад: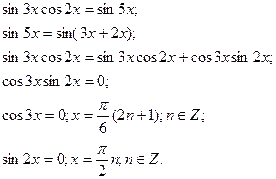

5.Рівняння виду .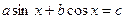

Зводимо до однорідного, враховуючи, що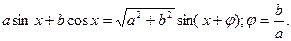

Наприклад: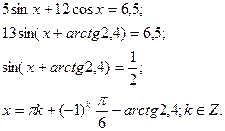

6.Рівняння, що розв’язуються перетворенням сум у добуток.

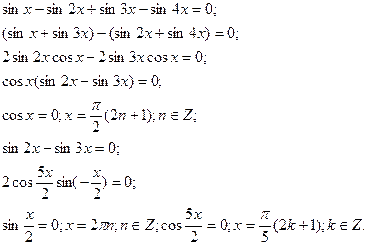
7.Рівняння, що розв’язуються перетворенням добутку двох тригонометричних функцій у суму.

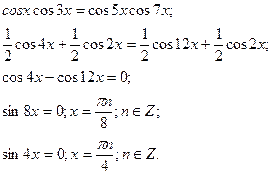
8.Рівняння, що розв’язуються пониженням степеня.

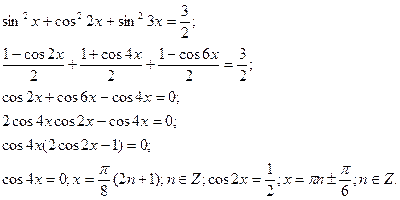
9.Рівняння виду .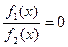

Лекція 11.

Тема: Системи тригонометричних рівнянь.

Розглянемо методи розв’язування тригонометричних рівнянь на конкретних прикладах.

1. Розв’язати систему рівнянь:

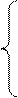А)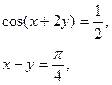

Розв’язання:

Зведемо систему до рівняння з одною змінною

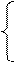
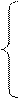
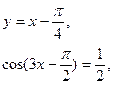
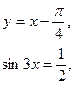
Відповідь:

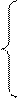Б)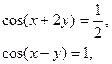

Розв’язання:

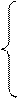
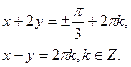
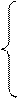Відповідь: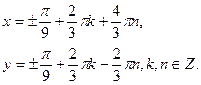

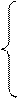
В)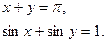

Розв’язання:

1)з першого рівняння

2) у другому рівнянні

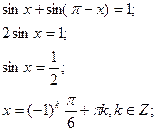
3)

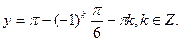
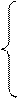Відповідь: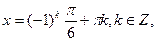

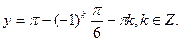
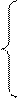Г)

Розв’язання:

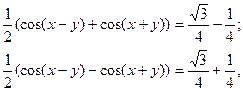
Спочатку додамо почленно рівняння системи, а потім віднімемо від першого друге

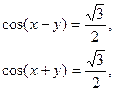
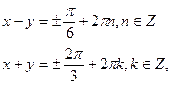
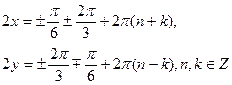
Відповідь: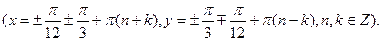

Лекція 12.

Тема: Найпростіші тригонометричні нерівності.

План.

1) .

2) .

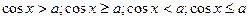3) .

1) .

2) .

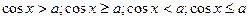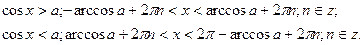
3) .

Модуль 2.

Лекція 13.

Тема: Корінь n-го степеня, його властивості, перетворення коренів, дії над коренями.

. План.

1. Означення кореня n-го степеня. Арифметичний корінь n-го степеня.

2. Властивості коренів n-го степеня.

3. Найпростіші перетворення коренів n-го степеня.

4. Дії над коренями.

Поиск по сайту: