Періодичність тригонометричних функцій

Функція називається періодичною з періодом Т 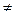0, якщо разом з х до області її визначення входить х Т і при цьому виконується умова .

Якщо Т-період функції, то nТ-теж її період, n .

Доведемо, що 2 -найменший додатний період синуса.

Метод від супротивного. Нехай є ще один період m<2 . , це можливо, коли

Але за припущенням n – ціле, тому .

Наприклад: Знайти найменший додатній період функції - числа.

Розв’язання:

Лекція 4.

Тема: Властивості тригонометричних функцій. Побудова графіків тригонометричних функцій.

Функція у = sin х

1. Область визначення: уся числова пряма.D(y):X=R

2. Область значень: відрізок [-1; 1].Е(y):Y=[-1;1].

3. Нулі функції: х=πn, n Z.

4.Парність і непарність:sin(-x) = -sin(x),

функція непарна для всіх х R. Г_sinсиметричний відносно точки О(0;0).

5Періодичність: sin(x+2π) =sin(x), функція періодична, Т = 2π.

6. Проміжки знакосталості:у > 0 для 2πn < x < π + 2π n, n Z.

у < 0 для π + 2 πn < х < 2π + 2πn, n Z.

7. Інтервали монотонності: у зростає на відрізках

у спадає на відрізках .

8. Найбільше та найменше значення:

при ; при

9. Інтервали опуклості: опукла вгору для 2πn <х< π + 2 πn, n Z;

опукла вниз для π + 2πn <х<2π + 2πn, n Z.

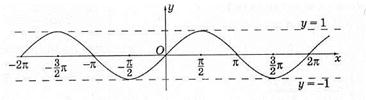
Графіком функції у=sinx є сину­соїда (мал. 8).

Функція у=cos х

1. Область визначення:D(y):X=R.

2. Область значень: відрізок [-1; 1].E(y):Y = [-1;1].

3. Нулі функції: .

4.Парність і непарність: cos(-x)= cos(x),

функція парна для всіх х R. Г_{соs х} симетричний відносно осі О у.

4. Періодичність:cos(x+2π)=cosx, функція періодична, Т = 2π.

6. Проміжки знакосталості: у>0 для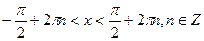

у < 0 для

7. Інтервали монотонності: у зростає на відрізках [-π+ 2πn; 2πn], n Z.

у спадає на відрізках [2πn; π+ 2πn], n Z.

8. Найбільше та найменше значення:
max у=1 при х=2πn, n Z; min у=-1 при х=π +2πn, n Z.

9. Інтервали опуклості:
опукла вгору для

опукла вниз для

Для побудови косинусоїди вико­ристовують те, що .

Мал.9

Функція у = tg х

1. Область визначення: множина R. .

2. Область значень:E(y):Y=R

З. Нулі функції: х=2πn, n Z.

4. Парність і непарність:tg(-x)=-tgx функція непарна для всіх х D(y).

Г_{tg x} симетричний відносно точки O(0; 0).

5. Періодичність: tg(x+π)=tg x, функція періодична, Т = π.

6. Проміжки знакосталості:y>0 для х

y<0 для х

7. Інтервали монотонності: у зростає на проміжках .

8. Функція у=tg х не має екстремумів

9. Інтервали опуклості: опукла вгору для ;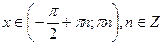

опукла вниз для

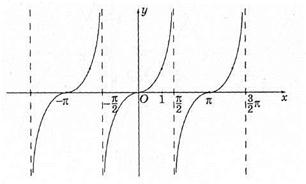
Графік функції у=tg х називають тангенсоїдою.

Мал. 10.

Функція y=ctg x

Властивості функції:

1. Область визначення: D(y):X = R\{πn}, n Z.

2. Область значень:E(y):Y = R.

3. Нулі функції: у=0 для ,

4. Парність і непарність:ctg(-x)=-ctg x, функція непарна для всіх х D(y).

5. Періодичність:ctg(x +π) = ctg х, функція періодич­на, Т =π.

6. Проміжки знакосталості: y>0 для х

y<0 для х

7. Інтервали монотонності: у спадає для .

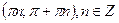8. Функція у=ctg х не має екстре­мумів.

9. Інтервали опуклості: опукла вгору для

опукла вниз для

Для побудови графіка у=ctgх ви­користовують те, що .

Отже, котангенсоїда — це зсунута на 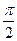праворуч тангенсоїда, у якої відповідні координати змінені на про­тилежні.

Лекція № 5.

Тема: Співвідношення між тригонометричними функціями одного аргументу. Тригонометричні тотожності додавання.

Основні тригонометричні тотожності