АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Тригонометричні функції числового аргументу

Читайте также:
  1. III. Соціальна політика, її сутність і функції.
  2. АБСТРАКТНІ КЛАСИ І ЧИСТІ ВІРТУАЛЬНІ ФУНКЦІЇ_________________________________________
  3. Автоматизоване робоче місце бухгалтера (АРМБ): призначення, функції та його рівні.
  4. Автоматизоване робоче місце бухгалтера (АРМБ): призначення, функції та його рівні.
  5. Алгоритм знаходження функції, оберненої до даної.
  6. АРГУМЕНТУВАННЯ
  7. Банківська система. Банки, їх види та функції
  8. Банківська система. Банки, їх види та функції
  9. Біржова торгівля. Товарна та фондова біржа, їх функції та значення
  10. Бухгалтерські рахунки, їх призначення, функції і побудова
  11. Бюджетно-податкова політика забезпечує найважливіші економічні функції держави, які формують її дієздатність в економічній політиці:
  12. Вектор-функція скалярного аргументу

Нехай у прямокутній системі координат х О у задано коло О (0; R).

Мал. 3.

Точка А належить колу (0; R), здійснює поворот на кут α в додатному напрямі в точку В (-х; у), 3 курсу геометрії відомо, що в прямокутному ΔВОС C = 90°, , , ,

Зі співвідношень видно, що значення синуса, косинуса, тангенса і котангенса залежать від а, але не залежать від R. Тому R можна вважати рівним 1.

Коло радіуса 1 з центром у початку координат називатимемо одиничним колом.

 

Мал. 4.

 

1. Ординату точки Pα одиничного кола, яку дістали при повороті точки Рα (1; 0) на кут радіан, називають синусом кута α sinα=у, (-l у 1)

2. Абсцису точки Рα одиничного кола, яку дістали при повороті точки Рα(1; 0) на кут радіан, називають косинусом кута α. соsα=х, (-l х 1)

3. Тангенсом кута α називають відношення: , , .

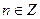4. Котангенсом кута a називають відношення: , , .

 

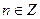5. Секансом кута a називають відношення: ,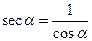

 

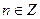
6. Косекансом кута а називають відношення: , , .

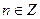Надалі вважатимемо, що всі кути виміряні в радіанній мірі, і тому позначення рад, як правило, опус­кається. Домовившись уважати одиницю вимірювання кутів (1 ра­діан) фіксованою, ми дістали мож­ливість розглядати тригонометричні функції числового аргументу.

Наприклад: синус числа х — це си­нус кута в х радіан; косинус числа х – косинус кута в х радіан і т. д.

Поставивши відповідно до кожного дійсного числа х його синус (або коси­нус, або тангенс, або котангенс, або се­канс, або косеканс), дістанемо функції:

у = sin х, у = cos х, у = tg х,

y = ctgx, y = secx, y = cosecx.

 

Для розв'язання ряду задач до­цільно ознайомитися з лінією танген­сів та лінією котангенсів.


Мал. 5.

 

 

1. Проведемо дотичну l до кола О (0; 1) у точці Ро(1; 0). Нехай х — довільне число, для якого cos 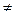0. Тоді точка Рх (cos x; sin x) (Оу), а тому пряма ОРх перетне l у точці Sx, абсциса якої хs=1.

Знайдемо ординату ys. Прямій ОРх належать точки О (0; 0), Рх (cos x; sin x). Отже, маємо рів­няння .

tgx = у => пряма l є лінією тангенсів.

2. Проведемо дотичну α до кола О (0; 1) у точці N(0; 1). Пряму α називають лінією котангенсів.


Знаки тригонометричних функцій Мал.6.

Значення тригонометричних функцій деяких кутів

Функція Значення кута в радіанах
 
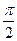
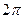
sin α       -1  
cos α     -1    
tg α        

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)