 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Введення поняття комплексного числа
При розв’язанні квадратних алгебраїчних рівнянь виникла проблема тоді, коли дискримінант  виявлявся числом від’ємним, і стало зрозуміло, що дуже корисно і зручно не ігнорувати символ
виявлявся числом від’ємним, і стало зрозуміло, що дуже корисно і зручно не ігнорувати символ  і вирази
і вирази  (де
(де  ), а оперувати з ними (чисто формально!), як із звичайними числами. А саме, якщо позначити
), а оперувати з ними (чисто формально!), як із звичайними числами. А саме, якщо позначити  та оперувати з виразами
та оперувати з виразами  за звичайними правилами
за звичайними правилами
 (5.1)
(5.1)
то при цьому виконуються всі звичайні властивості додавання та множення. Отже, з цієї точки зору вирази  мають таке саме право називатися числами, як вираз
мають таке саме право називатися числами, як вираз  (де
(де  ) – раціональними числами, або нескінченні десяткові дроби – дійсними числами.
) – раціональними числами, або нескінченні десяткові дроби – дійсними числами.
Якщо вважати, що  – це просто дійсне число а, що і – це
– це просто дійсне число а, що і – це 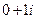 , то у відповідності з (5.1)
, то у відповідності з (5.1)  і, отже, вираз
і, отже, вираз  утворюється з
утворюється з  та
та  шляхом заданого в (5.1) алгоритму множення та додавання, тобто
шляхом заданого в (5.1) алгоритму множення та додавання, тобто 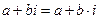 .
.
Отже, будь-яке квадратне рівняння виду 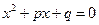 , де р і q – дійсні числа, має два корені, тобто:
, де р і q – дійсні числа, має два корені, тобто:
§ якщо дискримінант 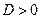 , то дане рівняння має два різних дійсних кореня
, то дане рівняння має два різних дійсних кореня  ;
;
§ якщо дискримінант  , то дане рівняння має два рівних дійсних кореня
, то дане рівняння має два рівних дійсних кореня 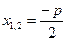 ;
;
§ якщо дискримінант  , то дане рівняння має два різних комплексних кореня
, то дане рівняння має два різних комплексних кореня
 .
.
Приклади. 5.1. Розв’язати рівняння  .
.
… Знаходимо дискримінант  .
.
За останньою формулою маємо  , або
, або  та
та  . †
. †
5.2. Розв’язати рівняння  .
.
… Знаходимо дискримінант  , отже
, отже  . †
. †
Подібне твердження відоме під назвою „основна теорема алгебри”, доведення якої було дане Гаусом в кінці XVIII ст., має місце для алгебраїчних рівнянь будь-якого ступеня з довільними комплексними коефіцієнтами.
Таким чином, ми отримуємо своєрідне розширення множини дійсних чисел, породжене приєднанням до R уявного елементу  , тобто такого, що
, тобто такого, що  .
.
Поиск по сайту: