 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Диференціювання оригіналів (зображення похідних оригіналів)
|
Читайте также: |
Зображення похідної 
оригіналу 
, якщо – оригінал, можна знайти за відомим зображенням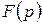 
оригіналу на підставі наступної теореми:
Теорема: Якщо, 
і – оригінал, то 
(6.8.1)
Доведення
На підставі означення зображення записується
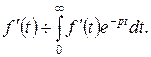
Шляхом інтегрування за частинами маємо:
тобто 
тому що в напівплощині 
буде:
при 
.
В окремому випадку, коли 
, формула (6.8.1) має вигляд:
(6.8.2)
Таким чином, якщо початкове значення оригіналу дорівнює нулю, диференціювання оригіналу приводить до множення його зображення на параметр р. Застосувавши формулу (5.8.1) до другої похідної 
, одержуємо:
Аналогічно
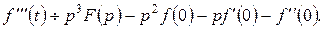(6.8.3)
……………………………………………………
В окремому випадку, коли 
буде
(6.8.4)
Поиск по сайту: