АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Інтегрування зображення

Читайте также:
  1. Властивість лінійності зображення
  2. Геометричне зображення комплексного числа. Модуль та аргумент комплексного числа
  3. Головні властивості і геометрична сутність картографічного зображення.
  4. Графічне зображення варіаційних рядів
  5. Графічні зображення символів та їх функції
  6. Графічні зображення схем
  7. Диференціювання зображення
  8. Диференціювання оригіналів (зображення похідних оригіналів)
  9. Зображення на картах об’єктів місцевості.
  10. ЗОБРАЖЕННЯ СИНУСОЇДНИХ ВЕЛИЧИН ВЕКТОРАМИ НА ПЛОЩИНІ
  11. Інтегрування оригіналів(зображення інтегралів)

Теорема: Якщо і – оригінал, то

тобто ділення оригіналу на аргумент 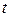веде до інтегрування зображення.

Доведення

Позначимо . Нехай 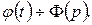Внаслідок того, що 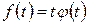, за теоремою диференціювання зображення . Далі за теоремою єдності 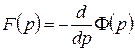, звідки де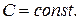

Довільна стала С визначається за умовою , а саме:

або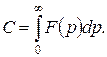

Отже: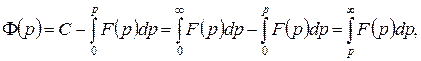

тобто:

(6.6.1)

Приклад 1. Знайти зображення оригіналу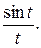

Розв¢язання

Внаслідок того, що застосовуючи формулу (5.6.1), маємо

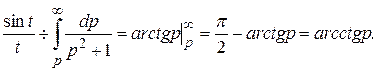
Приклад 2. Знайти зображення оригіналу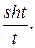

Розв¢язання

Відомо, що тому

Відповідь:

або


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |

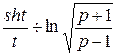
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)