Інтегрування оригіналів(зображення інтегралів)

Теорема: Якщо , то .

Доведення

Позначення , а значить , приводить за теоремою єдності і теоремою диференціювання оригіналу до рівності: де а Таким чином, звідки маємо:

(6.9.1)

Приклад. Якщо , то за теоремою інтегрування оригіналу

.

Відповідь:

.

Зауваження. Формули диференціювання й інтегрування оригіналів, тобто формули (5.8.1) і (5.9.1), що визначають зображення похідної й інтеграла від оригіналу , відіграють найважливішу роль в операційному численні, бо з них випливає, що діям вищого аналізу – диференціюванню й інтегруванню функцій-оригіналів, відповідають алгебраїчні дії – множення і ділення відповідно їхніх зображень 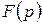на параметр р. Отже, величину р можна формально розглядати як оператор диференціювання, а величину – як оператор інтегрування функції-оригіналу на відрізку .

Слід також зазначити, що зображення значної кількості функцій-оригіналів, що зустрічаються на практиці, є дробово-раціональними алгебраїчними функціями параметра р.

Зазначене тут дає можливість багато задач вищого аналізу (розв¢язання диференціальних, інтегральних і інтегро-диференційних рівнянь і т.п.) звести до виконання алгебраїчних дій над зображеннями 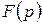шуканих функцій-оригіналів , які є розв¢язками таких задач.

Поиск по сайту: