Інтеграл по комплексній змінній

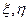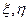Нехай на комплексній площині z задана кусочно-гладка крива С кінцевої довжини L. Використовуючи параметричне подання кривої С, задамо координати кожної її точки рівняннями , де — кусочно гладкі функції дійсного параметра t, що змінюється в межах ( можуть відповідно приймати значення ± ), що задовольняють умові . Завдання координат точок цієї кривої С еквівалентно завданню комплексної функції дійсної змінної t.

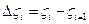Нехай у кожній точці кривої С визначене значення функції . Важливим поняттям у теорії функцій комплексної змінної є поняття інтеграла від функції по кривій С. Це поняття вводиться в такий спосіб. Розіб'ємо криву С на n часткових дуг точками ділення відповідним зростаючим значенням параметра t (). Уведемо позначення й складемо суму

(1.12)

де — довільна крапка i-й часткової дуги.

Якщо при 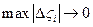існує межа сум, не залежний ні від способу розбивки кривій С, ні від вибору точок , то ця межа називається інтегралом від функції за кривою С і позначається як

(1.13)

Питання існування інтеграла (1.13) зводиться до питання про існування деяких криволінійних інтегралів від дійсної u і мнимої v частин функції f(z). Справді, записавши де 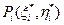- точка кривої С на площині xy, ми можемо представити вираження (1.12) у вигляді

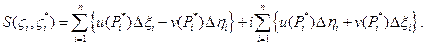
Дійсна й мнима частини являють собою інтегральні суми криволінійних інтегралів другого роду

(1.14)

відповідно, звідки й треба висловлене твердження.

Отже, інтеграл (1.20) представимо у вигляді

(1.15)

Це співвідношення може саме служити визначенням інтеграла від функції f(z) по кривій С. З нього витікає ряд властивостей, що є очевидним наслідком відповідних властивостей криволінійних інтегралів:

1.

2.

3. Якщо а - комплексна постійна, то

4.

5.

де ds — диференціал довжини дуги кривій С, а інтеграл, що розташований праворуч, є криволінійним інтегралом першого роду.

6. Має місце наступна формула заміни змінної інтегрування:

де — аналітична функція , що встановлює взаємно-однозначну відповідність між кривими С и Г. Зокрема,

де z = z(t) є параметричне завдання кривої С, a суть початкова й кінцева крапки останньої.

Приклад. У якості істотного для подальшого приклада обчислення інтеграла по комплексній змінній розглянемо інтеграл

,

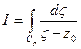де крива Ср являє собою окружність радіуса р із центром у крапці , обходжену проти вартовий стрілки. Скориставшись параметричною формою завдання кривій Ср: одержимо

Звідси слідує, що інтеграл не залежить ні від , ні від .

Оскільки значення контурного інтеграла залежить від напрямку інтегрування, умовимося як позитивний напрямок обходу контуру приймати напрямок, при якому внутрішня область, обмежена даним замкнутим контуром, залишається ліворуч від напрямку руху. Інтегрування в позитивному напрямку будемо позначати символом 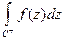або просто , інтегрування в негативному напрямку – символом .

Властивості інтегралів по замкнутому контурі від функцій, аналітичних усередині області, обмеженої даним контуром, багато в чому визначаються відомими властивостями криволінійних інтегралів другого роду. Як відомо, для криволінійних інтегралів по замкнутому контурі має місце наступне твердження: якщо функції Р(х,у) і Q(x,y) безперервні в замкнутій області , обмеженої кусочно гладким контуром С, а їхні частки похідні першого порядку безперервні в , то

(1.16)

Перейдемо тепер до основного положення інтегрування функції комплексної змінної

Теорема Коші. Нехай в однозв'язної області задана однозначна аналітична функція f(z). Тоді інтеграл від цієї функції f(z) за будь-яким замкнутим контуром Г, що цілком лежить в області , дорівнює нулю.

Отже, ця теорема встановлює факт рівності нулю інтеграла від аналітичної функції по будь-якому замкнутому контурі, що цілком лежить в однозв'язної області її аналітичності. При додатковій умові безперервності функції в замкнутій області дане твердження справедливо й для замкнутого контуру, що є границею області аналітичності. Останнє твердження фактично є трохи видозміненим формулюванням теореми Коші.

Невизначений інтеграл. Важливим наслідком теореми Коші є наступне положення. Нехай функція f(z) є аналітичною функцією в однозв'язної області . Фіксуємо в цій області деяку точку й позначимо через інтеграл по якій-небудь кривій, що цілком лежить в і з'єднуючої крапки z й . У силу теореми Коші цей інтеграл не залежить від вибору кривої інтегрування в області і є однозначною функцією z:

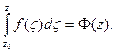(1.17)

Теорема. Нехай функція f(z) визначена й безперервна в деякої однозв'язної області , а інтеграл від цієї функції по будь-якому замкнутому контурі Г, що цілком лежить у даній області, дорівнює нулю. Тоді функція є аналітичною функцією в області й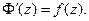

Доведена теорема дозволяє ввести поняття невизначеного інтеграла функції комплексної змінної. Аналітична функція називається первісною функції f(z) в області , якщо в цій області має місце співвідношення 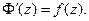. Очевидно, функція f(z) має множину різних первісних, але, як легко довести, всі первісні цієї функції розрізняються між собою лише постійними доданками. Сукупність всіх первісні функції f(z) називається невизначеним інтегралом від функції f(z).

Так само, як й у випадку функції дійсної змінної, має місце

(1.18)

де F(z) — будь-яка первісна функції f(z). Дійсно, інтеграл, що коштує ліворуч, не залежить від шляху інтегрування. Тому його можна представити у вигляді

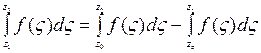, (1.19)

де — довільна точка області .

У якості істотного для подальшого приклада розглянемо функцію

Тому що підінтегральна функція є аналітичною на всій комплексній площині z, за винятком крапки z = 0, то вираження має сенс за умови, що крива інтегрування не проходить через крапку z = 0. При цьому в будь-якої однозв'язної області комплексної площини, що не містить точку z = 0, функція f(z) є однозначною аналітичною функцією z, що не залежить від вибору шляху інтегрування. Як така область будемо розглядати повну комплексну площину z, розрізану по від’ємній частини дійсної осі, тобто область . Будемо вважати, що шлях інтегрування у формулі лежить цілком в області , тобто не перетинає розрізу й не проходить через крапку z = 0. Тоді для дійсних додатних значень z = х, вибравши як шлях інтегрування у формулі відповідний відрізок дійсної осі одержимо .

Тобто для позитивних значень свого аргументу функція f(z) збігається з логарифмічною функцією дійсної змінної. Тому для функції в області () збережемо колишнє позначення, поклавши Остання рівність (у якому шлях інтегрування вибирається зазначеним вище способом) можна розглядати як визначення логарифмічної функції для всіх комплексних значень її аргументу, за винятком значень, що лежать на негативній частині дійсної осі z = х 0. Має місце співвідношення

Поиск по сайту: