 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Інтегральний спосіб
Способи детермінованого факторного аналізу, які ґрунтуються на принципі елімінування, мають спільний суттєвий недолік: при їх використанні виходять із того, що фактори змінюються незалежно один від одного. Однак, в дійсності, зміна одного фактора породжує зміну всіх інших, фактори змінюються одночасно, у взаємному зв’язкові. Від цієї взаємодії утворюється додаткова зміна результативного показника, яка при застосуванні способів елімінування приєднується до впливу одного з факторів (як правило, до останнього) на зміну результативного показника. Як наслідок дещо знижується результат впливу тих факторів, заміна (підстановка) яких проводиться раніше, за рахунок завищення результату останньої підстановки.
Отже, величина впливу факторів на зміну результативного показника змінюється залежно від місця того чи іншого фактора в детермінованій факторній моделі.
Проблему утворення додаткової зміни результативного показника від взаємодії факторів розглянемо на умовному прикладі. Нехай У = А х В – двофакторна мультиплікативна модель. Загальна зміна результативного показника (DУ) дорівнює сумі змін за рахунок факторів А (DУА) і В (DУВ):
DУ = DУА + DУВ. (5.89)
Насправді при розкладанні загальної зміни результативного показника отримують не два, а три компоненти:
DУ = У1 – У0 = А1хВ1 – А0хВ0 = (А0 + DА) х (В0 +DВ) – А0хВ0 =
= А0хВ0 + А0хDВ + DАхВ0 + DАхDВ – А0хВ0 =
= DАхВ0 + DВхА0 + DАхDВ. (5.90)
Останній параметр рівняння (DАхDВ) називається «нерозподіленим залишком», економічний зміст якого полягає у представленні сукупного одночасного впливу двох факторів А і В на зміну результативного показника У. Цей параметр, згідно із способами елімінування, не має права на самостійне існування й приєднується до величини впливу останнього фактора моделі.
З метою подолання зазначених недоліків у детермінованому факторному аналізі використовуються більш досконалі способи: інтегральний і логарифмічний.
Інтегральний спосіб дозволяє уникнути недоліків, властивих способам елімінування, тому що в цьому разі результати факторного аналізу не залежать від місця розташування факторів у моделі, а додаткова зміна результативного показника, яка утворилася від взаємодії факторів, розподіляється між ними пропорційно ізольованому їх впливу на результативний показник. При застосуванні інтегрального способу користуються робочими формулами для розрахунків, які наводяться у спеціальній літературі з економічного аналізу.
1. Для мультиплікативних моделей:
а) У = А х В. (5.91)
DУА = DА х В0 + ½ DА х DВ; (5.92)
DУВ = DВ х А0 + ½ DА х DВ. (5.93)
б) У = А х В х С. (5.94)
DУА = ½DА х (В0 х С1 + В1 х С0) + ⅓ DА х DВ х DС; (5.95)
DУВ = ½DВ х (А0 х С1 + А1 х С0) + ⅓ DА х DВ х DС; (5.96)
DУС = ½DС х (А0 х В1 + А1 х В0) + ⅓ DА х DВ х DС. (5.97)
2. Для кратних моделей:
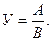 (5.98)
(5.98)
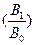
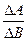
 DУА= ℓn; (5.99)
DУА= ℓn; (5.99)
DУВ = DУ - DУА . (5.100)
3. Для змішаних моделей:
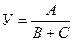 . (5.101)
. (5.101)
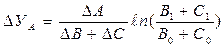 |
; (5.102)
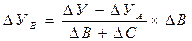 |
; (5.103)
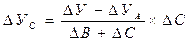 |
. (5.104)
Поиск по сайту: