АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Перша теорема розвинення

Читайте также:
  1. S-M-N-теорема, приклади її використання
  2. Вкажіть номер правильної відповіді. Перша хімічна токсична речовина, яку було використано німцями в 1915 г. проти англо-французьких військ?
  3. Внешние эффекты (экстерналии). Теорема Коуза.
  4. Внешние эффекты, их виды и последствия. Теорема Коуза
  5. Вопрос 1 теорема сложения вероятностей
  6. Вопрос 24 Теорема Остроградского-Гаусса для электрического поля в вакууме
  7. Вопрос. Теорема Котельникова (Найквиста)
  8. Второй закон термодинамики. Энтропия. Закон возрастания энтропии. Теорема Нернста. Энтропия идеального газа.
  9. Господарство в період державно-монополістичного розвитку суспільств європейської цивілізації (перша половина ХХ ст.)
  10. Гранична теорема Пуассона
  11. Дискретизація сигналу – теорема відліків (Котельникова)
  12. Донаукова фаза. Меркантилізм - перша школа економічних знань

Теорема: Якщо зображення 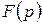являє собою степеневий ряд за від¢ємними степенями р з ненульовим радіусом збіжності, тобто, якщо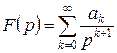

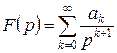(6.10.1)

то оригіналом зображення 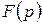є степеневий ряд за невід¢ємними степенями 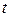, тобто

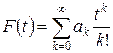(6.10.2)

який збігається при усіх .

Очевидно, що формальна відповідність рядів (5.10.1) і (5.10.2) мається, бо .

Доводиться, що ряд (6.10.2) сходиться рівномірно і його сума дорівнює оригіналу для функції .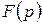

Приклад 1. Знайти оригінал функції

Розв¢язання

Функція є сумою степеневого ряду, що збігається при , тобто

Отже, на підставі першої теореми розвинення, маємо:

.

Відповідь:

.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)