АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема зсуву

Читайте также:
  1. S-M-N-теорема, приклади її використання
  2. Вимірювання кута фазового зсуву з перетворенням його на код
  3. Вимірювання кута фазового зсуву з перетворенням його на струм чи напругу
  4. Вимірювання кута фазового зсуву методом зрівноважуючого перетворення
  5. Вимірювання кута фазового зсуву осцилографічними методами
  6. Внешние эффекты (экстерналии). Теорема Коуза.
  7. Внешние эффекты, их виды и последствия. Теорема Коуза
  8. Вопрос 1 теорема сложения вероятностей
  9. Вопрос 24 Теорема Остроградского-Гаусса для электрического поля в вакууме
  10. Вопрос. Теорема Котельникова (Найквиста)
  11. Второй закон термодинамики. Энтропия. Закон возрастания энтропии. Теорема Нернста. Энтропия идеального газа.
  12. Гранична теорема Пуассона

Теорема: Якщо 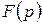є зображення функції , то 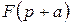– зображення функції 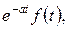тобто, якщо , то 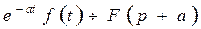(Тут передбачається, що ).

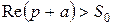Доведення

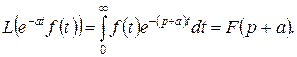(6.4.1)

Приклад 1. Знайти зображення функцій 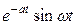і .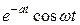

Розв¢язання

З формули 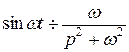на підставі теореми зсуву випливає:

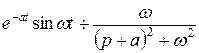
Аналогічно, з формули на підставі теореми зсуву:

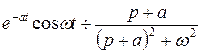
Теорема зсуву може розглядатися і як одна зі зворотних теорем, що дозволяють знаходити оригінали за заданими їх зображеннями. А саме, якщо відомо оригінал для зображення 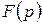, то формула 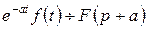дозволяє знайти оригінал для зображення 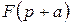, аргумент якого зміщений на .

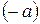Приклад 2. Знайти оригінал за зображенням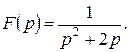

Розв¢язання

У силу формули 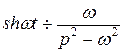і теореми зсуву, виділивши в знаменнику повний квадрат по р, маємо:

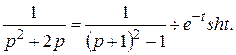
Відповідь:

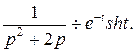
Приклад 3. Знайти оригінал, зображення якого задається формулою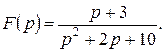

Розв¢язання

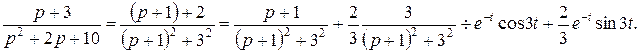
Відповідь:

 


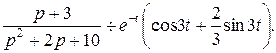
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)