Поняття функції комплексної змінної. Безперервність

Однозначна функція комплексної змінної z, задана в області G, визначається законом, що ставить кожному значенню z з області G у відповідність певне комплексне число . Символічно зазначена відповідність будемо записувати у вигляді .

Множина комплексних чисел w, що відповідають усім , називається множиною значень функції f(z). Оскільки кожне комплексне число характеризується парою дійсних чисел, то завдання комплексної функції w =u+iv комплексної змінної z = х +iу еквівалентно завданню двох дійсних функцій двох дійсних змінних, що може бути записане у вигляді w(z) =и(х, у) + iv(x, у).

Функції u(х,у) і v(x,y) визначені в області G площини дійсних змінних x, y, що відповідає області G комплексної площини z. Функція u(х,у) називається дійсною, а функція v(x,y) — мнимою частиною функції w = f(z).

Множина значень w функції f(z) на комплексній площині w може мати найрізноманітнішу структуру. Зокрема, це може бути область G або замкнута область . Надалі ми будемо розглядати тільки такі випадки.

Завданням функції w = f(z) установлюється відповідність між точками області комплексної площини z і точками області G комплексної площини w. Говорять, що при цьому задане відображення області на область G. Очевидно, установлюється й зворотна відповідність — кожній точці ставиться у відповідність одна або кілька точок z області . В останньому випадку можна говорити, що в області G задана багатозначна функція комплексної змінної w. Функція, що здійснює відображення області G комплексної площини w на область комплексної площини z, називається зворотною функцією f(z) 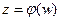є однозначною в області G. Тоді функція w = f{z) здійснює взаємно однозначне відображення області на область G.

Перейдемо до поняття безперервності функції комплексної змінної.

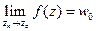Нехай функція f(z) визначена на деякій множині Е. Розглянемо різні послідовності точок цієї множини , що сходяться до деякої точки й складаються із точок відмінних від точки (), і відповідні їм послідовності значень функції . Якщо незалежно від вибору послідовності існує єдина межа , то ця межа називається граничним значенням, або межею, функції f(z) у точці , що записується у вигляді .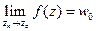

Функція f(z), задана на множині Е, називається безперервною в точці , якщо граничне значення цієї функції в точці існує, звичайне й збігається зі значенням функції f(z) у точці , тобто .

Якщо функція f(z), задана на множині Е, безперервна у всіх точках цієї множини, то говорять, що функція f(z) безперервна на множині Е.

Геометрично це означає, що функція комплексної змінної, безперервна в деякій точці , ставить у відповідність кожній точці з -околиці точки деяку точку, що належить 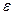-околиці точки .

З безперервності функції комплексної змінної f(z) =u(х,у) + iv(x,y) витікає безперервність її дійсної u(х,у) і мнимої v(x,y) частин по сукупності змінних x,у. Має місце й зворотне твердження, тобто якщо u(х,у) і v(x,y) суть безперервні функції по сукупності змінних x,у у деякій точці , то f(z)=u)x,y)+iv(x,y) є функцією комплексної змінної z = x+iy, безперервної в точці . Дані твердження є наслідком того, що необхідною й достатньою умовою збіжності послідовності комплексних чисел є збіжність послідовностей їх дійсних і мнимих частин.

Це дозволяє перенести на функції комплексної змінної основні властивості безперервних функцій двох дійсних змінних. Так, сума й добуток двох функцій комплексної змінної й , безперервних в області G, також є безперервними функціями в цій області; функція безперервна в тих крапках області G, де , функція f(z), безперервна на замкнутій множині , обмежена по модулі на й т.д.

Поиск по сайту: