АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Піднесення в ступінь і добування кореня з комплексного числа

Читайте также:
  1. Алгебраїчна форма запису комплексних чисел та дії над комплексними числами, записаними у цій формі
  2. Алгебраїчна форма комплексного числа
  3. Алгоритм получения дополнительного k-разрядного кода отрицательного числа
  4. Арифметические операции над двоично-десятичными числами
  5. Архівування, видобування об’єктів
  6. Байта орнамента числа числа
  7. В каком случае испытуемые должны были лучше запоминать числа и почему?
  8. В таблице показана зависимость частоты генерированного переменного тока от количества магнитных полюсов и числа оборотов генератора
  9. Введення поняття комплексного числа
  10. Во-вторых, увеличение числа актов снижает воздействие кульминаций и приводит к многочисленным повторениям.
  11. Водородоподобные атомы. Энергетические уровни. Квантовые числа.
  12. Выбор политики комплексного оперативного управления оборотными активами и краткосрочными обязательствами

Тригонометрична й показова форми запису комплексного числа зручні при розгляді алгебраїчних операцій піднесення комплексного числа в цілую позитивний ступінь і добування кореня з комплексного числа. Так, якщ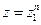о , то .

Комплексне число 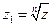називається коренем n-й ступеня з комплексного числа z, якщо 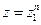. Із цього визначення треба, щоб . Як було відзначено вище, аргумент комплексного числа визначений не однозначно, а з точністю до адитивного що складає, кратного 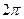. Тому з вираження для аргументу комплексного числа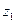 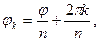де 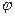— одне зі значень аргументу комплексного числа z, одержимо, що існують різні комплексні числа, які при піднесенні в n- ю ступінь рівні тому самому комплексному числу z. Модулі цих комплексних чисел однакові й рівні , а аргументи розрізняються на число, кратне 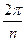. Число різних значень кореня n-й ступеня з комплексного числа z дорівнює n. Точки на комплексній площині, що відповідають різним значенням кореня n-й ступеня з комплексного числа z, розташовані у вершинах правильного n-кутника, уписаного в окружність радіуса із центром у точці z= 0. Відповідні значення 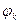виходять при k, що приймає значення k=0,1,…,n-1...


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)