АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема множення зображень (теорема про згортку)

Читайте также:
  1. S-M-N-теорема, приклади її використання
  2. Б) Множення вектора на скаляр
  3. Блок множення Product
  4. Внешние эффекты (экстерналии). Теорема Коуза.
  5. Внешние эффекты, их виды и последствия. Теорема Коуза
  6. Вопрос 1 теорема сложения вероятностей
  7. Вопрос 24 Теорема Остроградского-Гаусса для электрического поля в вакууме
  8. Вопрос. Теорема Котельникова (Найквиста)
  9. Второй закон термодинамики. Энтропия. Закон возрастания энтропии. Теорема Нернста. Энтропия идеального газа.
  10. Гранична теорема Пуассона
  11. Дискретизація сигналу – теорема відліків (Котельникова)
  12. Друга теорема економіки добробуту та її значення

Теорема: Якщо оригінал 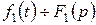, а оригінал 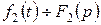, то

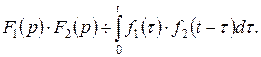(6.7.1)

Доведення

Позначивши 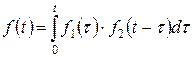, за визначенням зображення за Лапласом

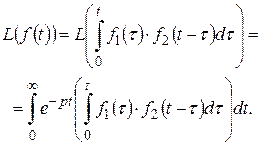(6.7.2)

Інтеграл, що стоїть праворуч, є подвійний інтеграл, який береться по області 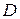, обмеженій прямими і при цьому:

 
 

 

 


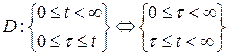
Зміна порядку інтегрування в інтегралі праворуч у рівності (6.7.2) дає:

.

Отже

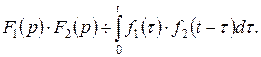
Інтеграл 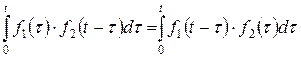називається згорткою функцій і і позначається .

Отже оригінал, що відповідає добутку двох зображень, дорівнює згортці оригіналів співмножників.

Приклад 1. Застосовуючи теорему множення зображень, знайти оригінал, якщо,

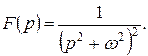
Розв¢язання

Маємо

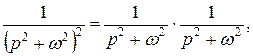
причому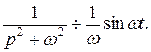

Тому, враховуючи, що

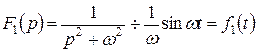
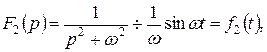
знаходимо:

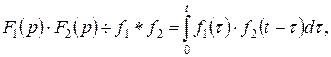
тобто

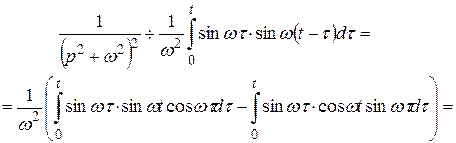
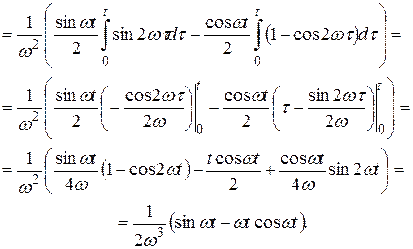
Відповідь:

.

Приклад 2. (самостійно). Застосовуючи теорему про згортку, знайти оригінал, якщо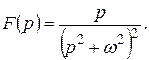

Відповідь:


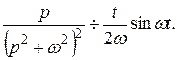
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)