Геометрична інтерпретація комплексних чисел

Оскільки комплексне число визначається як пара дійсних чисел, те природною геометричною інтерпретацією є зображення комплексного числа z = а + ib точкою площини ху з декартовими координатами х = а й у = b. Число z = 0 ставиться у відповідність початку координат даної площини. Таку - площина ми надалі будемо називати комплексною площиною, вісь абсцис — дійсної, а вісь ординат — мнимою віссю комплексної площини. При цьому, мабуть, установлюється взаємно однозначна відповідність між множиною всіх комплексних чисел і множиною крапок комплексної площини, а також між множиною всіх комплексних чисел z = a+ib і множиною вільних векторів, проекції х и у яким на осі абсцис й ординат відповідно рівні а й b.

Дуже важливою є також інша форма подання комплексних чисел. Для визначення положення крапки на площині можна користуватися полярними координатами де - відстань крапки від початку координат, а 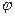- кут, що становить радіус-вектор даної крапки з позитивним напрямком осі абсцис. Позитивним напрямком зміни кута 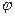вважається напрямок проти вартовий стрілки 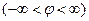.Скориставшись зв'язком декартових і полярних координат: , одержимо так називану тригонометричну форму запису комплексного числа:

(1.3)

При цьому звичайно називають модулем, а 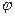— аргументом комплексного числа й позначають . Попередні формули дають вираження дійсної й мнимої частин комплексного числа через його модуль й аргумент. Легко виразити модуль й аргумент комплексного числа через його дійсну й мниму частини: 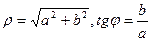(при виборі з рішень останнього рівняння значення 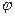варто врахувати знаки а й b). Відзначимо, що аргумент комплексного числа визначений не однозначно, а з точністю до адитивного що складає, кратного .

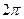Два відмінних від нуля комплексні числа рівні між собою в тім і тільки в тому випадку, якщо рівні їхні модулі, а значення аргументів або рівні, або відрізняються на число, кратне .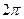

Комплексно сполучені числа мають той самий модуль, а значення їхніх аргументів, при відповідному виборі областей їхньої зміни, розрізняються знаком.

Нарешті, використовуючи відому формулу Ейлера , одержуємо показову форму запису комплексного числа: (1.4)

Рисунок 1- Операції над векторами

Відзначене вище відповідність між множиною всіх комплексних чисел і плоских векторів дозволяє ототожнити операції додавання й вирахування комплексних чисел з відповідними операціями над векторами (рисунок 1). При цьому легко встановлюються нерівності трикутника:

(1.5)

Модуль різниці двох комплексних чисел має геометричний сенс відстані між відповідними крапками на комплексній площині. Відзначимо, крім того, очевидні нерівності .

Для виконання операції множення зручно користуватися тригонометричною формою подання комплексних чисел. Відповідно до правил множення одержуємо

(1.6)

звідси, 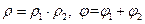, тобто модуль добутку дорівнює добутку модулів, а аргумент — сумі аргументів співмножників. У випадку ділення комплексних чисел при має місце аналогічне співвідношення:

(1.7)

Поиск по сайту: