 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Комплексне число та дії над ним
| Стор. | |
| Вступ……………………………………………………………………... | |
| Змістовий модуль 1. Елементи систем механізації........................ | |
| Тема 1.1 Загальні поняття, визначення та класифікації......................... | |
| Тема 1.2. Підйомно-транспортні машини неперервної дії.................... | |
| Тема 1.3 Підйомно-транспортні машини періодичної дії...................... | |
| Змістовий модуль №2. Основи робототехніки. Синтез систем механізації................................................................................................... | |
| Тема 2. Роботи і маніпулятори................................................................. | |
| Тема 3. Синтез систем механізації........................................................... | |
| Література.................................................................................................................... |
Вступ
Операційне числення широко застосовується на практиці при розв’язанні різних задач науки і техніки. Особливо широке застосування воно має при дослідження перехідних процесів у лінійних фізичних системах електротехніки, автоматики, радіотехніки і телемеханіки.
Сучасний математичний апарат операційного числення дозволяє розв'язувати задачі математичними моделями яких є системи лінійних диференціальних рівнянь (звичайних і з частними похідними), різницеві і диференційно-різницеві рівняння та деякі типи інтегральних рівнянь. Велика універсальність операційного числення при розв’язанні задач пояснюється можливістю отримати їх розв’язки найбільш раціональним шляхом.
В методичному посібнику наведені відповіді на теоретичні питання по курсу “Операційне числення”.
1 Деякі питання теорії комплексної змінної
Комплексне число та дії над ним
Комплексним числом z називається пара дійсних чисел (a, b) із установленим порядком проходження чисел a й b. Це умовно записується у вигляді z = (а, b). Перше число а пари (а, b) називається дійсною частиною комплексного числа z і позначається символом а = Re z, друге число b пари (а, b) називається мнимою частиною комплексного числа z і позначається символом b = Im z.
Два комплексних числа 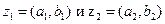 рівні тоді й тільки тоді, коли рівні їх дійсні й мнимі частини, тобто коли
рівні тоді й тільки тоді, коли рівні їх дійсні й мнимі частини, тобто коли 
Перейдемо до визначення алгебраїчних операцій над комплексними числами.
Сумою комплексних чисел 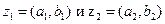 називається таке комплексне число z = (a, b), для якого
називається таке комплексне число z = (a, b), для якого  Легко бачити, що при такому визначенні зберігаються переміщувальний і сполучний закони додавання, тобто
Легко бачити, що при такому визначенні зберігаються переміщувальний і сполучний закони додавання, тобто  й
й  Так само, як й в області дійсних чисел, нулем називається таке комплексне число 0, сума якого з кожним комплексним числом z дорівнює цьому числу z, тобто z + 0 = z. Очевидно, що існує єдине комплексне число 0 = (0,,0), що володіє цією властивістю.
Так само, як й в області дійсних чисел, нулем називається таке комплексне число 0, сума якого з кожним комплексним числом z дорівнює цьому числу z, тобто z + 0 = z. Очевидно, що існує єдине комплексне число 0 = (0,,0), що володіє цією властивістю.
Добутком комплексних чисел 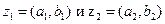 називається таке комплексне число z = (a, b), для якого
називається таке комплексне число z = (a, b), для якого  При такому визначенні добутку виконуються переміщувальний
При такому визначенні добутку виконуються переміщувальний  , сполучний
, сполучний 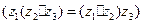 і розподільний
і розподільний  закони.
закони.
Включимо дійсні числа в множину комплексних чисел, розглядаючи дійсне число а як комплексне число а = (а,0). Тоді, як треба з визначення дій додавання й множення, для комплексних чисел зберігаються відомі правила дій над дійсними числами.
Тому множина комплексних чисел розглядається як розширення множини дійсних чисел. Помітимо, що множення на дійсну одиницю (1,0) не міняє комплексного числа: z * 1 = z.
Комплексне число виду z = (0, b) називається чисто - мнимим і символічно позначається як z = ib. Чисто уявне число (0, b) = ib можна розглядати як добуток мнимої одиниці (0,1) і дійсного числа (b,0). Мниму одиницю звичайно позначають символом (0,1) =i. У силу визначення добутку комплексних чисел справедливе співвідношення  Воно дозволяє додати прямий алгебраїчний зміст, так називаній алгебраїчній формі запису комплексного числа
Воно дозволяє додати прямий алгебраїчний зміст, так називаній алгебраїчній формі запису комплексного числа
 (1.1)
(1.1)
і робити операції додавання й множення комплексних чисел за звичайними правилами алгебри багаточленів.
Комплексне число z = а - ib називається комплексно сполученим числу z = а + ib.
Операція вирахування комплексних чисел визначається як операція, зворотна додаванню. Комплексне число z = a + ib називається різницею комплексних чисел 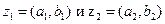 , якщо
, якщо 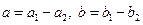
Операція ділення комплексних чисел визначається як операція, зворотна множенню. Комплексне число z = а + ib називається часткою комплексних чисел  , якщо
, якщо  з знаменником
з знаменником  відмінним від нуля.
відмінним від нуля.
 (1.2)
(1.2)
Поиск по сайту: