АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Дискретні випадкові величини і їх числові характеристики

Читайте также:
  1. I. Схема характеристики.
  2. V. Для дискретної випадкової величини Х, заданої рядом розподілу, знайти:
  3. Акустические колебания, их классификация, характеристики, вредное влияние на организм человека, нормирование.
  4. АКУСТИЧНІ ВЕЛИЧИНИ
  5. Амплітудна і фазова частотні характеристики
  6. Антикризисные характеристики управления персоналом
  7. Антропометричні характеристики людини
  8. Антропометричні характеристики людини.
  9. БАЗОВЫЕ ХАРАКТЕРИСТИКИ ОБЩЕСТВА
  10. Бюджетна система України: основні характеристики
  11. Величини
  12. Вибрация и ее характеристики

Найпростішою формою завдання закону розподілу дискретної випадкової величини Х є таблиця (матриця), в якій перелічувані в порядку зростання всі можливі значення випадкової величини і відповідні їм ймовірності

... ...
... ...

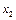
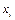
Х:
Така таблиця називається рядом розподілу дискретної випадкової величини.

Ряд розподілу може бути зображений графічно, якщо по осі абсцис відкладати

 
 

 


.

 

Закон розподілу числа з’явлення шістки відповідає біномному розподілу

Тоді

       

Х:

 

Закон розподілу цілком характеризує дискретну випадкову величину. Але часто закон розподілу буває невідомим або незручним для аналізу і тому приходиться обмежуватися меншими відомостями. Іноді вигідніше користуватися числами, які описують випадкову величину сумарно.

Числа, які призвані у стислій формі відтворювати найбільш характерні риси розподілу називаються числовими характеристиками випадкової величини.

Незважаючи на те, що сама величина Х – випадкова, її числові характеристики є величинами не випадковими, сталими.

Математичним сподіванням або середнім значенням дискретної випадкової величини Х називається сума добутків усіх її значень на відповідні їм ймовірності

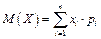(1.25)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)