Властивості дисперсії

1. Дисперсія сталої величини дорівнює нулю:

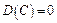
2. Сталий множник можна виносити за знак дисперсії, підносячи його до квадрата:

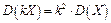
3. Дисперсія випадкової величини дорівнює різниці між математичним сподіванням квадрата випадкової величини і квадратом її математичного сподівання:

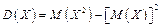(1.27)

4. Дисперсія алгебраїчної суми кінцевого числа незалежних випадкових величин дорівнює сумі їх дисперсій:

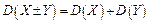
5. Дисперсія числа появи події 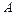в 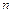незалежних випробуваннях, в кожнім з яких ймовірність 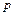появи події стала, дорівнює добутку числа випробувань на ймовірність появи і не появи події в одному випробуванні:

.

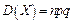Дисперсія 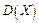має розмір квадрата випадкової величини, що не завжди зручно. Тому показником розсіювання використовують також величину .

Середнім квадратичним відхиленням (стандартним відхиленням або стандартом) випадкової величини Х називається арифметичне значення кореня квадратного з її дисперсії

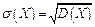(1.28)

Приклад 1.20. На шляху руху автомобіля чотири світлофори. Кожний з них з ймовірністю 0,5 або дозволяє, або забороняє автомобілю подальший рух. Побудувати многокутник розподілу ймовірностей випадкової величини, що відображує число світлофорів, які автомобіль пройде без зупинки. Чому дорівнюють математичне сподівання і дисперсія випадкової величини.

Розв’язання. Нехай випадкова величина Х – число світлофорів, які пройде автомобіль без зупинки. Ця величина може приймати наступні значення: 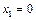, , 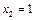, , 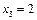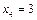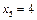.Ймовірність того, що число пройдених світло-

По цим даним будуємо многокутник розподілу ймовірностей (рис. 4).

Знайдемо математичне сподівання випадкової величини по її закону розподілу

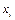
	0,5	0,25	0,125	0,0625	0,0625

Х:

Тоді використавши формулу (1.25), отримаємо:

.

Для визначення дисперсії дискретної випадкової величини визначимо спочатку 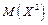, для чого складемо таблицю.

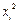
	0,5	0,25	0,125	0,0625	0,0625

Х²:

.

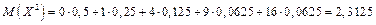Тоді за формулою (1.27) матимемо

.

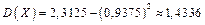Поиск по сайту: