АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Властивості інтегральної функції

Читайте также:
  1. III. Соціальна політика, її сутність і функції.
  2. А) Властивості бінарних відношень
  3. АБСТРАКТНІ КЛАСИ І ЧИСТІ ВІРТУАЛЬНІ ФУНКЦІЇ_________________________________________
  4. Автоматизоване робоче місце бухгалтера (АРМБ): призначення, функції та його рівні.
  5. Автоматизоване робоче місце бухгалтера (АРМБ): призначення, функції та його рівні.
  6. Алгоритм знаходження функції, оберненої до даної.
  7. Атрибутивні ознаки і властивості культури
  8. Б) Основні властивості операцій над множинами
  9. Банківська система. Банки, їх види та функції
  10. Банківська система. Банки, їх види та функції
  11. Біржова торгівля. Товарна та фондова біржа, їх функції та значення
  12. БУДОВА Й ЕЛЕКТРИЧНІ ВЛАСТИВОСТІ НАПІВПРОВІДНИКІВ

1. Значення інтегральної функції належать відрізку .

2. Інтегральна функція є неспадною функцією свого аргументу.

3. Ймовірність того, що випадкова величина прийме яке-небудь значення з інтервалу 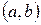, дорівнює приросту інтегральної функції на цьому інтервалі

.

Неперервні випадкові величини можна задавати за допомогою диференціальної функції.

Диференціальною функцією розподілу або густиною ймовірності називається перша похідна від інтегральної функції

Кривою розподілу неперервної випадкової величини називають графік її густини ймовірності.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)