АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Лінійна кореляція і рівняння лінійної регресії

Читайте также:
  1. А. Лінійна організаційна структура
  2. Бюджетні обмеження споживача, бюджетне рівняння та фактори впливу на бюджетну лінію.
  3. Геометричний зміст похідної. Рівняння дотичної.
  4. Грошовий обіг та його закони. Рівняння грошової та товарної мас (рівняння Ірвена Фішера). Грошові агрегати.
  5. Загальне рівняння фотосинтезу та походження кисню
  6. Змістовний модуль 6.2. «Рівняння, їх системи і сукупності.».
  7. Знаходження параметів лінійного рівняння регресії методом найменших квадратів
  8. Ковзаюче середнє (лінійна фільтрація)
  9. Коефіцієнт регресії та його властивості.
  10. КОМПЛЕКСНІ ХВИЛЬОВІ РІВНЯННЯ
  11. Лінійна філософія історії

 

Статистична залежність. При вивченні взаємозв’язків між різноманітними явищами часто з’ясовується, що кожному значенню однієї змінної відповідає кілька значень іншої, які зустрічаються не однаково часто.

Визначення. Якщо одному значенню змінної відповідає множина значень змінної , причому зазначена множина значень не залишається постійною, то говорять, що між змінними і існує статистична залежність.

Етапи кількісного вивчення кореляційного зв'язку:

1. Визначення тісноти (сили) зв’язку.

2. Побудова теоретичної лінії регресії (встановлення форм зв’язку).

3. Визначення значимості параметрів зв’язку.

Умовною середньою називають середнє арифметичне значень ознаки , що відповідають значенню .

Кореляційною залежністю від називають залежність умовної середньої від :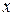

Це рівняння регресії на , 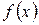– регресія на , графік 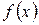– лінія регресії на . Найбільш простою формою взаємозв’язку є лінійна кореляційна залежність. Припустимо, що над ознаками і проведено спостережень, серед яких значення 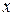зустрічається раз, значення – раз, пара чисел спостерігалася раз. Тому дані спостережень зручно представити в згрупованому виді – у виді кореляційної таблиці.

Рівняння прямої лінії регресії на має вид:

,

де – середня ознаки , – середня ознаки ,

– середня ознаки , – середня ознаки ,

– середнє квадратичне відхилення ознаки ,

– середнє квадратичне відхилення ознаки ,

 

Величина називається коефіцієнтом кореляції

.

Властивості коефіцієнта кореляції:

1о Абсолютна величина коефіцієнта кореляції не перевищує одиниці .
2о Якщо , то і не зв’язані лінійною кореляційною залежністю.
3о Зі збільшенням абсолютної величини коефіцієнта кореляції лінійна кореляційна залежність стає більш тісною і при перетворюється у функціональну залежність.

 

Коефіцієнт кореляції характеризує ступінь лінійної залежності між ознаками, тобто тісноту лінійного кореляційного зв’язку.

Якщо 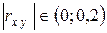, то між і практично відсутня лінійна кореляційна залежність.

Якщо , то між і існує слабка лінійна кореляційна залежність.

Якщо , то між і існує помітна лінійна кореляційна залежність.

Якщо , то між і суттєва лінійна кореляційна залежність.

Якщо , то між і існує тісна лінійна кореляційна залежність.

Якщо , то між і існує дуже тісна лінійна кореляційна залежність.

Якщо дані спостережень над ознаками і задані у виді кореляційної таблиці з рівновіддаленими варіантами, то для знаходження рівняння доцільно використовувати спрощену схему розрахунку. Ідея спрощення полягає в переході до більш простих значень змінних і виконання для них основних обчислень. Більш детально зазначену ідею реалізуємо на прикладі.

 

Приклад 19. Знайти рівняння прямої лінії регресії на по згрупованим даним кореляційної таблиці.

 

           
               
               
               
               
               
             

 

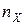
1. Об’єм вибірки . Значення показників і досить великі, рівновіддалені, можна перейти до більш простих, умовних варіант 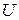і .

а) Вибирають найбільшу частоту в кореляційній таблиці – це 35. Відповідні цій частоті значення показників позначають через і :

.

б) Крок зміни значень показників позначають через і :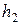

(на цю величину відрізняються значення ), (крок для ).

в) Визначають умовні варіанти за формулами:

 

 

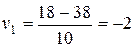
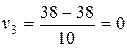
Після цього складають кореляційну таблицю в умовних варіантах, зберігаючи частоти.

 

– 3 – 2 – 1      
– 2              
– 1              
               
               
               
             

 

2. Проводять обчислення на основі умовних варіант.

а) для :

,

.

 

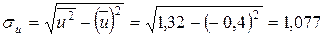б) для :

,

,

.

 

в) для і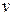

Знайдемо коефіцієнт кореляції:

.

Дане значення свідчить про високий ступінь взаємозв’язку показників 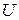і , а значить і .

 

3. Повертаємося до старих змінним і складаємо рівняння регресії.

,

,

,

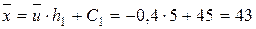– рівняння прямої лінії регресії на .

 

Порівняємо умовні середні, що знайдені по рівнянню (розрахункові значення) і за даними кореляційної таблиці (фактичні значення).

Розрахункові умовні середні:

Фактичні умовні середні

, , , , ,

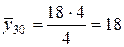Складемо таблицю

 

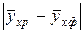
  17,59   0,41
  25,24 23,71 1,53
  32,89 34,67 1,78
  40,54 40,92 0,38
  48,19 46,57 1,62
  55,84   2,16

 

Узгодження розрахункових і фактичних умовних середніх задовільне.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.01 сек.)