Змістовний модуль 6.2. «Рівняння, їх системи і сукупності.»

ПЛАН.

1. Поняття рівняння з однієї змінною як предиката виду f(x)=g(x), де хєХ.

2. Рівносильні рівняння. Теореми про рівносильність рівнянь.

3. Рівняння з двома змінними. Рівняння лінії. Рівняння прямої та їх види.

4. Системи та сукупності рівнянь з двома змінними та способи (алгебраїчні та графічні) їх розв’язування.

5. Застосування рівнянь та їх систем до розв’язування текстових задач.

ЛІТЕРАТУРА: [1] – с. 238-293, 317-384; [2] – с. 53-59, 110-115, 294-355; [3] – с. 118-127.

1. Поняття рівняння з однієї змінною як предиката виду f(x)=g(x), де хєХ.

1. Розглянемо на множині Х два вирази із змінною f(х) і g(х). Утворимо предикат виду f(х)=g(х). Такий предикат називають рівнянням з однією змінною, при умові, що поставлено завдання знайти всі ті значення змінної хєХ, при підстановці яких у предикат одержуємо істинну числову рівність.

Означення: предикат виду f(х)=g(х), де хєХ, називається рівнянням з однією змінною, заданим на множині Х.

Прикладом рівняння з однією змінною можуть бути предикати х+5=9, х²+5х+6=0 тощо. Числові вирази при змінних у рівнянні називають коефіцієнтами, а інші числові вирази – вільними членами рівняння. Наприклад, у другому рівнянні число 5 є коефіцієнтом, а число 6 – вільним членом. Оскільки рівняння з однією змінною з предикатом, то, підставивши замість змінної у рівняння назву конкретного об’єкта х₀ із множини Х, одержимо істинне або хибне висловлення. Отже, рівняння визначає певний предикат з областю визначення Х. Саме тому основні поняття теорії рівняння можуть бути висвітлені з більш загальної точки зору – логіки предикатів.

Розв’язати рівняння – це означає знайти значення змінної х₀єХ, при підстановці яких у рівняння отримується істинна числова рівність. Таким чином, розв’язати рівняння – це означає знайти множину істинності відповідного предиката. Домовимося називати множину істинності предикату f(х)=g(х), де хєХ множиною розв’язків рівняння, а числа, які входять в цю множину, - коренями або розв’язками рівняння. Наприклад, рівняння х²+5х+6=0 має два розв’язки 2 і 3. Отже, множина розв’язків цього рівняння має вигляд Т={2;3}. Оскільки множина істинності предиката може бути порожньою, містити скінченну чи нескінченну кількість елементів, то рівняння може мати один, декілька, безліч або жодного розв’язку.

Оскільки рівняння є предикатом, то з ним пов’язано дві множини: а) множина Х допустимих значень змінної (множина визначення предикату); б) множина Т коренів рівняння (множина істинності предикату). Множина коренів рівняння є підмножиною множини допустимих значень змінної, тобто ТÌХ. Відносно рівняння може ставитися два завдання, по-перше, знайти область допустимих значень змінної, і, по-друге, знайти множину коренів рівняння. Покажемо це на наступній вправі.

Вправа: знайти множину допустимих значень та множину розв’язків рівняння .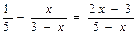

Розв’язання:

Для того, щоб знайти множину допустимих значень цього рівняння, з’ясуємо, які арифметичні операції є у рівнянні. Оскільки це операції додавання, віднімання, множення і ділення, серед яких не завжди виконується лише операція ділення, то множиною допустимих значень рівняння будуть ті хєR, при яких знаменники відмінні від нуля. Отже, 3-х≠0 і 5-х≠0, тобто х≠3 і х≠5. Тоді областю допустимих значень рівняння буде множина (-∞;3)È(3;5)È(5;+∞).

Для розв’язання рівняння 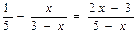зведемо його до спільного знаменника 5(3-х)(5-х). Тоді будемо мати таку систему:

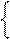(3-х)(5-х)-5х(5-х)-5(2х-3)(3-х)=0

(3-х)(5-х)≠0.

Враховуючи область допустимих значень рівняння, розкривши дужки у першому рівнянні системи та звівши подібні доданки, одержимо: 8х²-39х+30=0. Розв’язавши це квадратне рівняння та перевіривши чи належать одержані корені області допустимих значень, робимо висновок про множину коренів рівняння.

Поиск по сайту: