V. 2. Механічне описання молекулярної системи

Як уже відомо, в термодинаміці стан системи, що містить єдину речовину, цілком однозначно визначається в загальному випадку трьома незалежними змінними. Наприклад, числом молів (n), енергією (U) і об’ємом (V). Проте з мікроскопічної точки зору така система, скажемо, 1 моль якої-небудь речовини містить біля 10²⁴ (до певної міри) окремо існуючих індивідуальних молекул. Статистична механіка ставить завдання описати стан кожної частинки шляхом зазначення її координат і характеру руху, що здійснюється. При цьому вважається, що рух молекул описується законами класичної механіки, що застосовуються у формі так званих канонічних рівнянь Гамільтона:

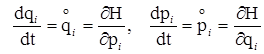, (V.2.1)

де H(p, q) = e (p, q) + U(q) – функція Гамільтона (гамільтоніан). Вона рівна повній енергії системи, тобто сумі кінетичної енергії e (p, q) і потенціальної U(q);

Застосовуючи уявлення класичної механіки до молекулярних систем, атом уподібнюється матеріальній точці і йому приписують три ступені свободи (число ступенів свободи – число незалежних змінних, що визначають положення механічної системи в просторі). Передбачається при цьому, що атоми як класичні механічні об’єкти можна розрізняти і вони можуть бути,,пронумеровані“. Положення і-го атому можна задати радіусом-вектором з декартовими складовими x_i, y_i, z_i. Число ступенів свободи системи з N атомів складає 3N. Число ступенів свободи зменшується при виникненні між складовими системи зв’язків. При наявності К зв’язків число ступенів свободи стає рівним 3N–K. (Наприклад, для змодельованої жорсткої двохатомної молекули передбачається, що віддаль між атомами є сталою і К = 1, число ступенів свободи складатиме 5, тоді як в загальному випадку нежорсткої молекули це число буде рівним 6 і т. ін.)

Число ступенів свободи молекули позначимо f (для одноатомної молекули f = 3). Для системи з N молекул число ступенів свободи складе F = N× f, якщо всі молекули однакові, і , якщо є молекули n сортів (f_i – число ступенів свободи, N _i – число молекул сорту і).

Місцезнаходження і-ої частинки можна визначити також за допомогою так званих узагальнених координат. Узагальнені координати – будь-які змінні, сукупність яких достатня для визначення положення механічної системи в просторі, тобто задати координати всіх частинок, що утворюють систему. Узагальнені координати виберемо з урахуванням накладених на систему механічних зв’язків так, щоб число узагальнених координат рівнялось числу ступенів свободи. Набір узагальнених координат запишемо як q₁,…,q _f для молекули і q₁,…,q_{N f} для сукупності N молекул (в цьому випадку перші f координати відносять до і-тої молекули, наступні f, від (f + 1)-ої до 2 f – до 2-ої і т. д.). Скорочено цей набір позначають однією буквою q.

Швидкість зміни змінної при зміні механічного стану подається змінною , що називається і-ю узагальненою швидкістю (t – час, 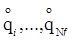(скорочено ) – набір узагальнених швидкостей.

В статистичній термодинаміці для описання механічного стану системи віддають перевагу змінним q _i i р _і; де р _і – і-тий узагальнюючий імпульс.

Надалі корисно уявити собі багатомірний простір з 2 f координатами, які можна назвати фазовим m -простором (для запам’ятовування: m -простір – простір молекули (m!). Точка в такому фазовому просторі вказує на,,стан“ частинки в момент часу t, а зміна цього стану в часі однозначно зобразиться в силу детермінованості законів класичної механіки деякою траєкторією руху зображеної точки. Наприклад, на площині можна подати фазовий простір для f = 1 і відповідну траєкторію, що відображає функцію часу

q = q(t) i p = p(t) (V.2.2)

В якості прикладу системи з f = 1 візьмемо гармонійний осцилятор, що володіє повною енергією Е. Як відомо, в цьому випадку

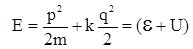(V.2.3)

де m – маса частинки, що коливається, q – зміщення від положення рівноваги, k – силова стала квазіпружної сили (закон Гука). З співвідношення (V.2.3) витікає, що фазова траєкторія в цьому випадку зобразиться еліпсом (рис. 11).

Для більш складної системи, наприклад газу, що містить N багатоатомних молекул, метод залишається, по суті, тим же. Тільки фазовий простір має вже 2N f вимірів і називається гамма-простором (g -простір). Точка в такому просторі зобразить миттєвий стан всієї системи в цілому, тобто дасть докладне описання кожної із частинок, що її складають – точне значення всіх 2N f -змінних. Відповідно траєкторія такої зображуваної точки являє розвиток розглянутої системи в часі. В цьому випадку траєкторія визначається 2N f рівняннями виду (V.2.2), тобто:

q _i = q(t); p _i = p(t) (i = 1, 2,3,…,N _f), (V.2.4)

які в свою чергу визначаються рівняннями руху Гамільтона (V.2.1).

Слід відмітити, що оскільки закони класичної механіки детерміновані, траєкторія, що виходить із даної точки, однозначно визначена. Строго кажучи, з цього витікає наслідок: траєкторія в фазовому просторі не може сама себе перетнути.

V. 3. Розподіл молекул за швидкостями та розподіл

імовірностей для швидкостей молекул

Користуючись методами статистичної механіки виявилось можливим створити досить просту модель, за допомогою якої можна достатньо точно передбачити властивості ідеальних газів. Щоб можна було обмежитись нескладними підрахунками, для такого газу прийнята проста модель, заснована на таких припущеннях: 1) об’єм, що займає газ, містить дуже велике число молекул; 2) молекули малі в порівнянні з віддалями між ними і знаходяться в стані безперервного руху, причому їх траєкторії між двома зіткненнями є прямими лініями; 3) молекули мають сферичну форму і взаємодіють одна з одною лише при співударах: співудари молекул одна з одною зі стінками посудини ідеально пружні, тобто ніяка частина енергії співударів не переходить у внутрішню енергію молекул (енергію руху їх частин).

Швидкість молекули змінюється при кожному її зіткненні з іншою молекулою газу, так що в кожний даний момент є деякий розподіл за швидкостями. При рівновазі цей розподіл миттєвих швидкостей не залежить від часу. Розподіл компоненти швидкості вздовж напрямку х (v _х) в кожний момент можна описати шляхом ділення вісі швидкостей на рівні відрізки Dv_х і визначення числа молекул, компоненти швидкостей v _х, які попадають у кожний з цих відрізків. На рисунку по вісі ординат зручно відкладати не частку молекул, що попадає в даний інтервал Dv_х а частку, що поділена на ширину інтервалу (рис. 12, а).

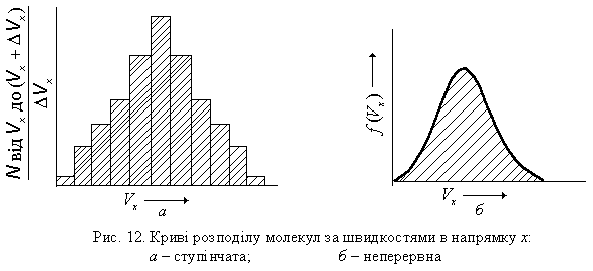
В цьому випадку площина кожного прямокутника на ступінчатому графіку є рівною частці молекул, що попадають у даний інтервал.

Картина виходить більш точною, якщо розглядати велику кількість молекул і зменшувати інтервал Dv _х. Тоді початковий ступінчатий графік поступово перетворюється в гладеньку криву. При безкінечно малих інтервалах швидкості частка молекул, що припадає на одиничний інтервал, може бути описана безперервною функцією f (v _х), яка називається функцією густини імовірності для швидкостей молекул. В цьому випадку частка молекул, швидкості яких знаходяться в межах від v _х до v _х + dv _х, рівна f (v _х)×dv _х. Множник dv _х з’являється тут, оскільки частка молекул, що припадає на даний інтервал швидкості dv _х, пропорційна ширині dv _х. Графік залежності f (v _х) від v _х, подібний до того, який поданий на рис. 12 (б), повністю описує розподіл молекул за швидкостями.

Розрахувати частку молекул газу, швидкості яких лежать в заданому інтервалі, можна за допомогою рівняння Больцмана. Якщо молекули знаходяться в станах з енергіями e₁, e₂ і т. д., то відповідне число молекул N₁, N₂ і т. д. в цих станах при рівновазі залежать від абсолютної температури Т. Таким чином:

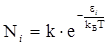, (V.3.1)

де N _i – число молекул з енергією e _і; значення константи k визначається з умови: åN _i = N (N – загальне число молекул у системі).

Показник степені фактора Больцмана містить відношення енергії молекули до енергії теплового руху k_БТ. Константа Больцмана, або молекулярна газова стала k_Б рівна сталій ідеального газу, розділеній на число Авогадро N_A; тобто:

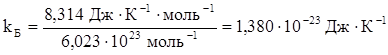
Для розгляду розподілу імовірностей для швидкостей молекул розглянемо спочатку розподіл імовірностей для швидкостей в напрямку х. Компонента кінетичної енергії для цього напрямку рівна і, отже згідно з рівнянням (V.3.1), частка молекул, швидкість яких вздовж напрямку х, що знаходиться в межах між v _х і v _х + dv_х (ця частка рівна f (v _х)dv_х), визначається рівнянням

(V.3.2)

Значення k¢ може бути визначене з таких міркувань. Із умови нормування , тоді

(V.3.3)

Зробимо заміну змінної: 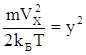. Тоді ; ; .

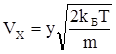Якщо V_X = 0, то і у = 0; якщо V_X = ¥, то і у = ¥. Тому (V.3.3) можна записати так:

.

Оскільки , то

або

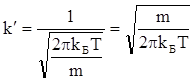(V.3.4)

Підставивши значення k¢ з (V.3.4) в (V.3.2) отримаємо співвідношення

(V.3.5)

Графік залежності f (V _х) від V _х, розрахований за цим рівнянням для випадку газоподібного дигідроґену при 273,16 К, поданий на рис. 12 (б). Ординати графіка дають імовірність того, що довільно обрана молекула буде володіти миттєвою швидкістю v _х, значення якої відкладені по осі абсцис. Розподіл молекул за швидкостями для напрямків y і z будуть такими ж, як і для напрямку х.

Розподіл молекул за величинами істинної швидкості складає значно більший інтерес, ніж розподіл їх по компонентах швидкості V _х, V _y і V _z в напрямку х, y і z. Щоб розглянути розподіл молекул за швидкостями, зручно зобразити швидкість і напрямок руху кожної молекули газу у вигляді вектора, паралельного напрямку руху, довжина якого пропорційна швидкості. Потім слід уявити, що вектори зсунуті так, що початком для всіх них є центр декартової системи координат. Довжина кожного вектора пов’язана з величинами його компонентів по трьох взаємно перпендикулярних напрямках таким співвідношенням:

(V.3.6)

Число точок в будь-якому безкінечно малому елементі об’єму dV_х×dV_y×dV_z, координати якого V_х, V_y, V_z, відповідає числу молекул, що мають швидкості з компонентами, які знаходяться між V_х і V_х + dV_х, V_y і V_y + dV_y, V_z і V_z + dV_z. Частка молекул, швидкості яких попадають в цей інтервал, рівна добутку трьох окремих імовірностей і може бути подана таким виразом

f(V_х, V_y, V_z)dV_х×dV_y×dV_z

Оскільки e ^a e ^b e ^c = e ^{a + b + c} , то

(V.3.7)

Зручно виразити це рівняння через загальну швидкість молекули (V), а не через компоненти швидкості в напрямку х, y і z. Безкінечно малий елемент об’єму dV_х×dV_y×dV_z можна записати у вигляді V²dVdw (dw – безкінечно мала зміна тілесного кута). Оскільки всі напрямки в просторі рівноцінні, то густина точок в тонкому сферичному шарі радіусом r повинна бути рівномірною. Розподіл молекул за швидкостями f(V)dV одержується шляхом інтегрування рівняння (V.3.7) за всіма значеннями тілесного кута від 0 до 4p. Вираз f(V)dV визначає імовірність того, що випадково обрана молекула має швидкість в інтервалі від V до V + dV:

(V.3.8)

Рівняння (V.3.8) було вперше виведене Максвелом у 1860 р. і має фундаментальне значення для кінетичної теорії газів.

V. 4. Підрахунок мікростанів та закон розподілу молекул за енергіями (закон Больцмана)

У системах, що складаються з великого числа однакових молекул, наприклад, 1 моль якого-небудь хімічно чистого газу, для описання механічного стану простіше застосовувати фазовий m -простір 2 f -вимірювань, якщо f – число ступенів свободи молекули. Точка в такому просторі буде точно визначати координати (q₁...q _f) і імпульси (р₁...р _f) даної єдиної молекули. Число вимірювань в g -просторі, що застосовується для опису стану системи в цілому, буде в N раз більшим, тобто рівним 2N f, якщо N – число молекул в системі. Якщо між молекулами системи відсутні (значні) сили взаємодії, то g -простір системи можна подати сукупністю індивідуальних m -просторів. Місце знаходження точки в g -просторі системи описує положення зображуваної точки кожної молекули в її власному m -просторі і визначає стан (мікростан) всієї системи в цілому. Очевидно також, що миттєвий мікростан системи N молекул буде характеризуватися розподілом зображуваних точок в m -просторі. З класичних позицій даному рівноважному макростану буде відповідати безкінечно велике число мікростанів, оскільки молекули весь час рухаються і стикаються, обмінюючись імпульсами.

Підрахунок числа мікростанів, тобто термодинамічної імовірності, зводиться до знаходження числа можливих способів розміщення всіх молекул по різних областях фазового простору. Конкретний обрахунок термодинамічної імовірності залежить від подальших припущень про області і частинки фазового простору. За класичною схемою Больцмана розмір областей невизначений, а частинки можна розрізнити. В квантових статистиках частинки вважаються такими, що не розрізняються, а області фазового простору передбачаються такими, що складаються з малих комірок. Розмір комірок визначається законами квантової механіки. Надалі будемо розглядати переважно ідеальні гази і користуватимемось статистикою Больцмана.

Нехай система складається з N молекул, а її макростану відповідає N₁ фігуративних точок у першій комірці, N₂ точок у другій і т. д., і в загальному випадку N _і точок і-й комірці. Оскільки перестановки в середині комірки не враховуються, то вони не дають нових мікростанів. Число останніх знаходиться як число з повтореннями

(V.4.1)

На наведеній вище схемі показані два,,макростани“: І – всі молекули знаходяться в одній комірці і ІІ – молекули розподілені рівномірно по всіх комірках. Число,,мікростанів“, що відповідає першому,,макростану“, рівна одиниці, тобто всі молекули в першій комірці, а перестановки в середині комірки не враховуються. Для другого,,макростану“ підраховують W за формулою (V.4.1)

,

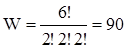тобто другий,,макростан“ згідно з класичною статистикою може бути одержаний 90 способами.

Дуже важливим є також закон, що описує розподіл молекул за енергіями в рівноважній молекулярній системі. Для виведення цього закону уявимо, що газоподібна система, яка вивчається, складається з дуже великого числа молекул (N). Вона володіє заданою повною енергією (внутрішньою (U), її в статистиці часто позначають Е) і займає сталий об’єм (V). Тож з термодинамічної точки зору система ізольована (U = const, V = const).

Припустимо, що всі молекули хімічно ідентичні, але можуть володіти різними енергіями. В найпростішому випадку це буде енергія поступального руху mv²/2, де v – швидкість руху молекули, m – її маса.

Розподіл молекул за енергіями можна записати в такий спосіб:

N₁, володіють енергією e₁,

N₂, володіють енергією e₂,

N₃, володіють енергією e₃,

і т. д.

Повна енергія розглянутої системи виразиться сумою:

(V.4.2)

що має, за умовою, стале значення. Сталим є і повне число молекул

(V.4.3)

(окремі числа N _i можуть змінюватись).

Якщо розглядати рівноважну ізольовану систему, що складається з N молекул, то за законом розподілу Больцмана число молекул N _i, які володіють енергією Е _і, пропорційне фактору Больцмана (V.3.1)

Якщо врахувати рівняння (V.4.3), то

, (V.4.4)

або

N = k×Z, (V.4.5)

де

, (V.4.6)

і називається сумою по станах.

Поиск по сайту: