За допомогою рівнянь (V.3.1) і (V.4.5) одержимо співвідношення

, (V.4.7)

яке показує, що сума по станах так відноситься до повного числа молекул, як фактор Больцмана до числа молекул, що володіють заданою енергією. Іншими словами, сума по станах є узагальнюючим фактором Больцмана.

Важливою властивістю суми по станах є мультиплетність. Вона може бути подана у вигляді добутку сум по станах, що відповідають окремим незалежним видам руху

Z = nZ_k, (V.4.8)

Переконаємось у справедливості цього для випадку, коли енергія молекул може бути подана у вигляді суми енергій поступального та обертового рухів (e _і = e_{пост, j} + e_{об, q} ).

Запишемо Z для даного випадку так

, (V.4.9)

Виносячи за знак однієї із сум члени, що не залежать від індексу сумування, одержимо

, (V.4.10)

або

Z = Z_пост · Z_об (V.4.11)

Встановимо, як змінюється сума по станах при зміні рівня відліку енергії. Замість абсолютного значення енергії e _і часто користуються енергією e = e₁ – e_о, що відраховується (обчислюється) від рівня енергії e_о, якою володіє молекула при температурі, що рівна абсолютному нулю (назвемо її нульовою енергією). Підставивши в рівняння (V.4.7) e₁ = e + e_о, одержуємо

, (V.4.12)

Винесемо за знак суми член, що не містить індексу сумування

, (V.4.13)

звідки

(V.4.14)

Вивчення спектрів показало, що в молекули може бути декілька рівнів з однаковою або близькою енергією. Такі кратні рівні називаються виродженими. В цьому випадку одній і тій же енергії відповідає декілька станів молекули, що відрізняються не енергією, а якоюсь іншою властивістю (наприклад, орієнтацією магнітного моменту). Існування вироджених рівнів стає причиною появи в рівнянні суми по станах однакових членів. Тому сума по станах набуває такого вигляду

, (V.4.15)

де q _i – число співмножників, що співпадають для рівня e _і і називається виродженністю рівня або його статистичною вагою.

V. 5. Молекулярна сума по станах

Молекула володіє різними видами енергії, головними із яких є поступальна, обертова, коливна й електронна. Для складних молекул при не дуже високих температурах наближено передбачають, що окремі види руху не впливають один на одного, а енергія молекули рівна

e = e_пост + e_об + e_кол + e_ел (V.5.1)

В цьому випадку сума по станах рівна добутку сум по станах для окремих видів руху

Z = Z_пост×Z_об×Z_кол×Z_ел (V.5.2)

При обчисленні суми по станах поступального руху ідеального газу молекула розглядається як частинка, що володіє лише масою і здатністю переміщуватись в просторі. Для такої молекули з енергією

, (V.5.3)

необхідно враховувати, що за де-Бройлем їй відповідає хвильовий рух з довжиною хвилі

, (V.5.4)

За умови квантування якщо рух молекули обмежується прямолінійною ділянкою l, то величина напівхвилі повинна вкладатись на цій ділянці ціле число раз. Тому , де n = 1, 2, 3,.... З цього витікає, що

, (V.5.5)

а рівні енергії дискретні і визначаються рядом квадратів цілих чисел.

Якщо молекула рухається в комірці, об’єм якої рівний добутку трьох відрізків V = l ₁× l ₂× l ₃, і переміщення її обмежується вздовж вісі координат, то внаслідок мультипликативності суми по станах матимемо

, (V.5.6)

Розглянемо газ, що містить N молекул в об’ємі V. Поступальну суму по станах (Q) цієї системи можна визначити, використовуючи суму по станах (Z_пост) окремих молекул, а саме: Q = Z .З іншого боку для обчислення Q можна застосовувати формулу (V.5.6), передбачаючи, що дана система є сукупністю молекул. Але треба врахувати, що молекули не відрізняються між собою. Тому в знаменник суми по станах системи слід ввести N!, маючи на увазі, що молекули не відрізняються між собою. Таким чином, одержуємо

, (V.5.7)

Звідси, примінивши формулу Стирлінга N! = N^N×e^–N, знаходимо більш точнішу молекулярну суму по станах для поступального руху

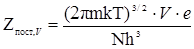, (V.5.7)

Визначивши молекулярну суму по станах не лише для поступального руху, а й обертового, коливного і електронного, можна розрахувати повну суму по станах.

Поиск по сайту: