 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Малюнок № 6.4
|
Читайте также: |
Якщо в загальному рівнянні прямої визначити у, то при В≠0 загальне рівняння прямої приймає вигляд  . Якщо позначити -
. Якщо позначити -  через
через  , а
, а 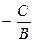 через
через  , то рівняння приймає вигляд
, то рівняння приймає вигляд  , тобто матиме вигляд рівняння прямої з кутовим коефіцієнтом. Якщо
, тобто матиме вигляд рівняння прямої з кутовим коефіцієнтом. Якщо  , то рівняння буде мати вигляд Ах+С=0 або х=а, тобто має рівняння прямої, паралельної осі ординат. Якщо А=0, то маємо рівняння Вх+С=0 або у=b, тобто рівняння прямої, паралельної осі абсцис.
, то рівняння буде мати вигляд Ах+С=0 або х=а, тобто має рівняння прямої, паралельної осі ординат. Якщо А=0, то маємо рівняння Вх+С=0 або у=b, тобто рівняння прямої, паралельної осі абсцис.
Запишемо умови паралельності і перпендикулярності прямих, заданих своїми загальними рівняннями. Нехай маємо дві прямі  та
та  . Якщо
. Якщо  і
і  , то
, то  ,
,  . Виходячи із умови паралельності прямих
. Виходячи із умови паралельності прямих 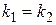 , маємо
, маємо  або –a1b2=-a2b1. Тоді умова паралельності запишеться так: a1b2-a2b1=0. Оскільки умова перпендикулярності прямих має вигляд k1k2=-1, то для прямих, які задані загальними рівняннями прямої, умова перпендикулярності матиме вигляд a1а2+b1b2=0.
або –a1b2=-a2b1. Тоді умова паралельності запишеться так: a1b2-a2b1=0. Оскільки умова перпендикулярності прямих має вигляд k1k2=-1, то для прямих, які задані загальними рівняннями прямої, умова перпендикулярності матиме вигляд a1а2+b1b2=0.
Нехай задано дві прямі  та
та  . Якщо ці прямі перетинаються, то координати точки перетину задовольняють обидва рівняння, а це означає, що для знаходження точки перетину двох прямих потрібно розв’язати систему рівнянь:
. Якщо ці прямі перетинаються, то координати точки перетину задовольняють обидва рівняння, а це означає, що для знаходження точки перетину двох прямих потрібно розв’язати систему рівнянь:  . Пропонуємо студентам самостійно розв’язати наступні вправи, використовуючи виведені раніше формули.
. Пропонуємо студентам самостійно розв’язати наступні вправи, використовуючи виведені раніше формули.
Вправа 1: Знайти точку перетину прямих  та
та  .
.
Вправа 2: Як розміщені прямі на площині?  та
та  .
.
Вправа 3: Записати рівняння прямої, яка проходить через точки  ,
, 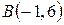 .
.
Вправа 4: Знайти тангенс кута між прямими  та
та  .
.
Поиск по сайту: