АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Малюнок № 6.3

Читайте также:
  1. Малюнок 1 Вікно Конструктора форм
  2. Малюнок 11.3.
  3. Малюнок 11.7.
  4. Малюнок 8.4.
  5. Малюнок 8.5.
  6. Малюнок № 1.
  7. Малюнок № 1.1.
  8. Малюнок № 10.1.
  9. Малюнок № 10.3.
  10. Малюнок № 11.10.
  11. Малюнок № 11.4.
  12. Малюнок № 11.8.

Проведемо тепер дві прямі, які не проходять через початок координат. Нехай це будуть прямі y=k1x+b1 і y=k2x+b2. Оскільки кутові коефіцієнти прямих y=k1x і y=k2x та y=k1x+b1 і y=k2x+b2 однакові, то пряма y=k1x і паралельна прямій y=k1x+b1, а пряма y=k2x паралельна прямій y=k2x+b2, які перпендикулярні між собою. Отже, перпендикулярними будуть і прямі y=k1x+b1 і y=k2x+b2. Тоді умовою перпендикулярності двох прямих, заданих рівняннями з кутовими коефіцієнтами буде наступна рівність k1k2= -1.

Наведемо без виведення ряд рівнянь прямої, які будуть потрібні при розв’язуванні задач (див. таблицю № 6.1.).

Виведемо формулу кута між двома прямими y=k1x+b1 і y=k2x+b2 (див. малюнок № 6.4.). Для цього пригадаємо, що кутовий коефіцієнт це тангенс кута нахилу прямої до осі абсцис. Із трикутника МНК видно, що , бо зовнішній кут трикутника МНК. Звідси 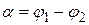. Отже, маємо: . Ця формула дозволяє знаходити кут між двома прямими, які задані своїми рівняннями з кутовими коефіцієнтами.

 

рівняння пучка прямих, що проходять через точку М0(х0;у0).
рівняння прямої, яка проходить через дві дані точки М1(х1;у1) та М2(х2;у2).
Загальне рівняння прямої.

 

Таблиця № 6.1. Види рівнянь прямої.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)