Обернена пропорційність, її властивості та графік

4. Розглядаючи прямо пропорційні величини, ми встановили, що вони задаються формулою у= kх. Сформулюємо означення обернено пропорційних величин.

Означення: дві величини називаються обернено пропорційними, якщо із збільшенням (зменшенням) однієї величини у кілька разів інша величина зменшується (збільшується) у стільки ж разів.

Означення: функцією оберненої пропорційності називається функція виду у=k/х, де k≠0 і kєR.

Розглянемо властивості функції у=k/х. Оскільки для знаходження значення у за відомим значенням х необхідно виконати дію ділення, яка в множині дійсних чисел не існує лише для ділення на нуль, то областю визначення цієї функції буде множина дійсних чисел крім нуля. Отже, D(k/x)=(-∞;0)È(0;+∞). Для визначення проміжків монотонності функції виберемо два довільних значення аргументу х₁ і х₂ таких, що х₁>х₂. Тоді 1/ х₁<1/х₂. Якщо k>0, то k/х₁>k/х₂, тобто f(х₁)<f(х₂). Це означає, що при k>0 функція оберненої пропорційності спадає на всій області визначення. Якщо k<0, то із нерівності 1/х₁<1/х₂ випливає k/х₁>k/х₂, тобто f(х₁)>f(х₂). Це означає, що при k<0 функція оберненої пропорційності зростає на всій області визначення.

Для того, щоб визначити парною чи непарною є ця функція, відповідно до означення непарних функцій маємо: f(-х)=k/(-x)= -k/x= -f(х), тобто справедлива рівність f(-х)= -f(х). Це означає, що функція у=k/х є непарною, а її графік повинен бути симетричним відносно початку координат. Із шкільного курсу математики відомо, що графіком функції у=k/х є гіпербола, яка розміщена у першій та третій координатних кутах, якщо k>0, і в другій та четвертій чверті, якщо k<0. Особливою точкою функції є точка з координатами (0;0). Якщо х прямує до нуля, залишаючись меншим за х, то при k>0 функція у=k/х прямує до -∞. Якщо ж х прямує до нуля, залишаючись більшим за нуль, то функція прямує до +∞. Якщо х прямує до нуля, залишаючись меншим за х, то при k<0 функція у=k/х прямує до +∞. Якщо ж х прямує до нуля, залишаючись більшим за нуль, то функція прямує до -∞. Оскільки для кожного значення аргументу х≠0 і хєR, можна знайти відповідне йому значення функції уєR, яке не дорівнює нулю, то множиною значень функції у=k/х є множина таких дійсних чисел, для яких хє(-∞;0)È(0;+∞), тобто Е(k/x)=(-∞;0)È(0;+∞).

5*. Квадратична функція, її властивості та графік.

5. Означення: функція виду y=ax²+bx+c, a,b,cєR, a≠0 називається квадратичною функцією.

Областю визначення квадратичної функції є множина всіх дійсних чисел, бо для знаходження значення функції за заданим значенням аргументу необхідно виконати дії додавання і множення, які в множині дійсних чисел завжди виконуються. Функція не відноситься ні до парних, ні до непарних, бо y(-x)=a(-x)²+b(-x)+c=ax²-bx+c=-(-ax²+bx-c), тобто не виконується жодна з рівностей f(-х)=f(х) чи f(-х)= -f(х).

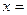
Знайдемо проміжки монотонності функції, виділивши попередньо повний квадрат: . Якщо a>0, то функція спадає на проміжку , а зростає на . Якщо a<0, то функція зростає на проміжку , а спадає на . При a>0 функція має найменше значення , при . При a<0 функція має найбільше значення при 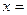, що дорівнює . Графіком функції є парабола, вітки якої при a>0 напрямлені вверх, а при a<0 – вниз. Множиною значень функції при a>0 є проміжок , а при a<0 - .

6*. Операції над функціями та графіками, перетворення графіків.

6*. У математиці досить часто доводиться розв’язувати питання про те, які ж операції можна виконувати над функціями, як при цьому зміниться область визначення D(f) функції, як побудувати графік нової функції. Для того, щоб знайти відповіді на поставлені запитання, розглянемо кілька нових понять.

Означення: сумою функцій f і g називають функцію f+g, яка визначена на множині D(f+g)=D(f)ÇD(g) та для якої виконується умова, що для будь-якого хєD(f+g) справедлива рівність [f+g](x)=f(x)+g(x).

Означення: добутком функцій f і g називають функцію f•g, яка визначена на множині D(f•g)=D(f)ÇD(g) та для якої виконується умова, що для будь-якого хєD(f•g) справедлива рівність f•g(x)=f(x)•g(x).

Для того, щоб одержати функції f+g чи f•g, якщо вони задані аналітично, слід додати чи помножити праві частини функцій. Проілюструємо це на конкретному прикладі.

Вправа: знайти суму та добуток даних функцій y₁=x³+3, хє[0;3] і у₂=3х+2, хє[0;6].

Поиск по сайту: