 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Властивості емпіричної функції
1. Значення емпіричної функції належать відрізку [0; 1]
F*(x)є [0; 1].
2. Емпірична функція F*(x) є неспадною функцією.
3. Якщо х1 – найменша варіанта, тоді F*(x)=0 при х<x1; якщо хk - найбільша варіанта, тоді F*(x)=1 при х>xk.
 Приклад:
Приклад:
Побудувати емпіричну функцію за даним розподілом вибірки

| |||

|
Рішення
Знайдемо обсяг вибірки п=12+18+30=60.
1. Так як xmin = 2, тоді за властивістю 2: F*(x)=0 при х<2.
2. Для х<6, х1=2, п1=12, тоді  при
при  .
.
3. Для х<10, х1=2, х2=6, п2=12+18=30, тоді 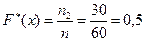 при
при  .
.
4.
5. Оскільки xmax = 10, тоді за властивістю 2 F*(x)=1 при х>10;
Тоді шукана емпірична функція має вигляд:

Побудуємо графік емпіричної функції

1 1.3. Графічна інтерпретація статистичного ряду
Для наочності будують різні графічні зображення статистичного розподілу, зокрема полігон і гістограму.
 Означення: Полігоном частот (відносних частот) називається ламана, відрізки якої з’єднують точки з координатами (х1,п1), (х2,п2),...,(хк,пк) або (х1,W1), (х2,W2),...,(хк,Wк).
Означення: Полігоном частот (відносних частот) називається ламана, відрізки якої з’єднують точки з координатами (х1,п1), (х2,п2),...,(хк,пк) або (х1,W1), (х2,W2),...,(хк,Wк).
Для побудови полігона частот на осі абсцис відкладають варіанти xi, а на осі ординат – відповідні їм частоти ni, або відповідні відносні частоти Wi.
 Приклад:
Приклад:
Побудувати полігон відносних частот наступного розподілу

| ||||

| 0,4 | 0,2 | 0,1 | 0,3 |
Рішення

 Означення: Гістограмою частот (відносних частот) називається східчаста фігура, яка складається з прямокутників, основами яких служать часткові інтервали довжиною h, а висоти дорівнюють відношенню
Означення: Гістограмою частот (відносних частот) називається східчаста фігура, яка складається з прямокутників, основами яких служать часткові інтервали довжиною h, а висоти дорівнюють відношенню  .
.
Площа гістограми частот дорівнює обсягу вибірки п, а відносних частот – одиниці.
 Приклад:
Приклад:
Статистичний розподіл задано таблицею
Частинний Частоти
інтервал
5-10 4
10-15 6
15-20 16
20-25 36
25-30 24
30-35 10
35-40 4
Побудувати гістограму частот даного розподілу.
Рішення
Для побудови гістограми складемо таблицю
Частинний Частоти Середина Висота
інтервал інтервалу стовпця
5-10 4 7,5 0,8
10-15 6 12,5 1,2
15-20 16 17,5 3,2
20-25 36 22,5 7,2
25-30 24 27,5 4,8
30-35 10 32,5 2,0
35-40 4 37,5 0,8

 Задача 11.3.1
Задача 11.3.1
Дано вибірку даних про складання іспиту з дисципліни „Вища математика” студентам спеціальності „Економіка підприємства”
2 3 3 2 5 4 4 2 5 4 3 2
5 4 3 2 2 4 3 2 2 4 3 2
2 3 4 5 4 3 5 4 3 5 4 3
2 4 3 2 3 4 3 3 4 3 4 4
4 3 4 3 4 3 4 3 4 4 4 3
3 4 4
Для даної вибірки:
1. Скласти варіаційний ряд та статистичний розподіл.
2. Знайти емпіричну функцію та побудувати її графік.
3. Побудувати полігон відносних частот.
4. Побудувати гістограму відносних частот.
Рішення
1. Для складання варіаційного ряду знайдемо найбільше і найменше значення функції та розмах

Оскільки розмах невеликий або розмах досить великий, але багато однакових варіант, то будемо складати дискретний розподіл. Для цього складемо варіаційний ряд (розташуємо кожну варіанту в порядку зростання) і підрахуємо для кожної варіанти відповідні частоти (кількість відповідних варіант). Одержані результати занесемо до таблиці (стовпчики 2 і 3 таблиці).
| № п/п | Варіанта хі | Частота пі | Відносна частота 
| Накопичена відносна частота

| Висота гістограми

|
| 1. | 0,19 | 0,19 | 0,19 | ||
| 2. | 0,33 | 0,52 | 0,33 | ||
| 3. | 0,38 | 0,90 | 0,38 | ||
| 4. | 0,10 | 1,00 | 0,10 | ||
| 5. | 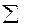
| 1,00 |
Обсяг вибірки п=63.
2. Знайдемо емпіричну функцію розподілу
Оскільки xmin = 2, тоді за властивістю 2 емпіричної функції: F*(x)=0 при х<2.
Для х<3, х1=2, п1=12, тоді  при
при  .
.
Для х<4, х1=2, х2=3, п2=12+21=33, тоді  при
при  .
.
Для х<5, х1=2, х2=3,х3=4 п2=12+21+24=57, тоді  при
при  .
.
Оскільки xmax = 5, тоді за властивістю 2 емпіричної функції: F*(x)=1 при х>5.
Тоді шукана емпірична функція має вигляд (дивись стовпчик 5 таблиці)

Побудуємо графік емпіричної функції

3. Побудуємо полігон відносних частот, тобто ламану, що з’єднує точки з координатами 

4. Побудуємо гістограму відносних частот, тобто східчасту фігуру з основою 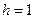 (відстань між сусідніми варіантами) і висотою
(відстань між сусідніми варіантами) і висотою  (дивись стовпчик 6 таблиці)
(дивись стовпчик 6 таблиці)

 Задача 11.3.2
Задача 11.3.2
Дано вибірку даних про вагу студентів спеціальності „Економіка підприємства”
58 63 59 59 67 53 53 69 68 55 67 53
45 73 50 66 59 54 68 58 90 72 51 71
63 55 81 46 44 58 59 61 44 53 74 65
63 62 51 63 67 59 67 65 62 69 81 75
52 70 49 72 60 56 71 52 44 77 47 51
66 72 90 73 56 69 78 63 69 74
Для даної вибірки:
1. Скласти варіаційний ряд, статистичний розподіл.
2. Знайти емпіричну функцію та побудувати її графік.
3. Побудувати полігон відносних частот.
4. Побудувати гістограму відносних частот.
Рішення
1. Для складання варіаційного ряду знайдемо найбільше і найменше значення функції та розмах

Оскільки розмах великий, то будемо складати неперервний розподіл. Для цього за формулою Стерджесса знайдемо кількість інтервалів, на які будемо розбивати розмах:
 , (11.2)
, (11.2)
де N – кількість інтервалів; п – обсяг вибірки.
Для нашої вибірки п=70, тому

Довжину інтервалу  визначаємо за формулою
визначаємо за формулою
 . (11.3)
. (11.3)
Довжина інтервалу для нашої вибірки  (округлення бажано робити до цілого парного числа).
(округлення бажано робити до цілого парного числа).
Після цього складемо варіаційний ряд (розташуємо кожний інтервал в порядку зростання) і підрахуємо для кожного інтервалу відповідні частоти (кількість відповідних варіант, причому в інтервал входить варіанта, що стоїть на початку інтервалу і не входить та, що стоїть у кінці). Одержані результати занесемо до таблиці (стовпчики 2 і 3 таблиці).
| № п/п | Інтервал хі – хі+1 | Частота пі | Середина інтервалу хі* | Відносна частота 
| Накопичена відносна частота

| Висота гістогра-ми 
|
| 1. | 44 - 50 | 0,10 | 0,10 | 0,017 | ||
| 2. | 50 - 56 | 0,19 | 0,29 | 0,032 | ||
| 3. | 56 - 62 | 0,17 | 0,46 | 0,028 | ||
| 4. | 62 - 68 | 0,21 | 0,67 | 0,035 | ||
| 5. | 68 - 74 | 0,20 | 0,87 | 0,033 | ||
| 6. | 74 - 80 | 0,07 | 0,94 | 0,012 | ||
| 7. | 80 - 86 | 0,03 | 0,97 | 0,005 | ||
| 8. | 86 - 92 | 0,03 | 1,00 | 0,005 | ||
| 9. | 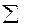
| 1,00 |
Обсяг вибірки п=70.
2. Знайдемо емпіричну функцію розподілу.
Оскільки xmin = 44, тоді за властивістю 2 емпіричної функції: F*(x)=0 при х<44.
Для х<50, х1=[44; 50), п1=7, тоді  при
при  .
.
Для х<56, х1=[44;50), х2=[50;56), п2=7+13=20, тоді  при
при  .
.
Для х<62, х1=[44;50), х2=[50;56), х3=[56;62) п3=7+13+12=32, тоді  при
при  .
.
Для х<68, х1=[44;50), х2=[50;56), х3=[56;62), х4=[62;68) п4=7+13+12+15=47, тоді  при
при  .
.
Для х<74, х1=[44;50), х2=[50;56), х3=[56;62), х4=[62;68), х5=[68;74) п5=7+13+12+15+14=61, тоді 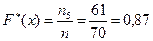 при
при  .
.
Для х<80, х1=[44;50), х2=[50;56), х3=[56;62), х4=[62;68), х5=[68;74), х6=[74;80) п6=7+13+12+15+14+5=66, тоді  при
при  .
.
Для х<86, х1=[44;50), х2=[50;56), х3=[56;62), х4=[62;68), х5=[68;74), х6=[74;80), х7=[80;86) п7=7+13+12+15+14+5+2=68, тоді  при
при 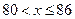 .
.
Для х<92, х1=[44;50), х2=[50;56), х3=[56;62), х4=[62;68), х5=[68;74), х6=[74;80), х7=[80;86), х8=[86;92) п8=7+13+12+15+14+5+2+2=70, тоді  при
при  .
.
Оскільки xmax = 92, тоді за властивістю 2 емпіричної функції: F*(x)=1 при х>92.
Таким чином, шукана емпірична функція має вигляд (дивись стовпчик 5 таблиці):

Побудуємо графік емпіричної функції

3. Побудуємо полігон відносних частот, тобто ламану, що з’єднує точки з координатами 
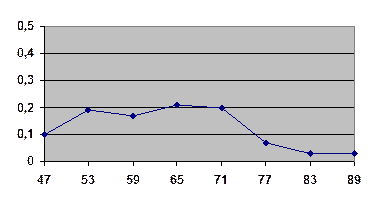
4. Побудуємо гістограму відносних частот, тобто східчасту фігуру з основою 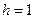 (відстань між сусідніми варіантами) і висотою
(відстань між сусідніми варіантами) і висотою  (дивись стовпчик 6 таблиці)
(дивись стовпчик 6 таблиці)

Розділ 11.4. Завдання до заняття 11
 Теоретичні питання до розділу 11
Теоретичні питання до розділу 11
1. Сформулювати основні задачі математичної статистики.
2. Дати означення генеральної та вибіркової сукупності.
3. Що називається обсягом виборки?
4. Дати означення відносної частоти.
5. Дати означення варіаційного ряду.
6. Дати означення статистичного розподілу.
7. Яка функція називається емпіричною?
8. Сформулювати властивості емпіричної функції.
9. На вашу думку, що є аналогом емпіричної функції в теорії ймовірностей?
10. Дати означення полігону частот і полігону відносних частот.
11. Дати означення гістограми частот і гістограми відносних частот.
Розділ 12.1. Генеральна та вибіркова середні. Властивості середньої
 Означення: Генеральною середньою називається середнє арифметичне значень ознаки генеральної сукупності. Вибірковою середньою називається середнє арифметичне значень ознаки вибіркової сукупності.
Означення: Генеральною середньою називається середнє арифметичне значень ознаки генеральної сукупності. Вибірковою середньою називається середнє арифметичне значень ознаки вибіркової сукупності.
Надалі ми не будемо уточнювати про який вид середньої йдеться, а будемо називати її середньою арифметичною.
Середня арифметична визначається за формулою:
1) якщо всі варіанти різні 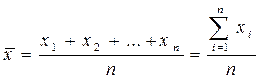 ; (12.1)
; (12.1)
2) якщо варіанти зустрічаються з певними частотами
 , (12.2)
, (12.2)
де п – обсяг генеральної або вибіркової сукупності.
 Приклад:
Приклад:
Генеральна сукупність задана таблицею розподілу
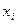
| ||||||
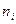
|
Знайти генеральну середню.
Поиск по сайту: