Задачі до розділу 5.1

Задача 5.1.1

Ймовірність появи події в кожному з 100 незалежних випробуваннях однакова і дорівнює 0,8. Знайти ймовірність того, що подія з’явиться не менше 75 раз і не більше 90 раз.

Рішення

За умовою задачі: Оскільки п досить велике, то за інтегральною теоремою Лапласа

,

.

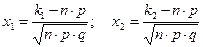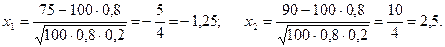
Враховуючи, що функція Лапласа є непарною, тобто Ф(-х)=-Ф(х), маємо

Тоді за формулою (5.2) шукана ймовірність дорівнює

Задача 5.1.2

У страховій компанії 10 тис. клієнтів, які застрахували своє майно. Страховий внесок складає 2000 грн., ймовірність нещасного випадку р= 0,005, страхова виплата клієнту у нещасному випадку складає 200 тис. грн. Визначити розмір прибутку страхової компанії з ймовірністю 0,95.

Рішення.

Нехай у – страхові виплати при нещасних випадках. Тоді прибуток компанії є різницею між сумою страхових внесків і сумою страхових виплат, тобто

.

Задача полягає у знаходженні такого числа N, для якого ймовірність нещасного випадку не перевищувала 1-р, іншими словами повинна виконуватися умова

.

Визначимо значення аргументу функції Ф(х) при

,

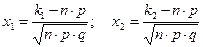За таблицею функції Лапласа знаходимо, що тому що х>5. За формулою (5.2)

,

За таблицею функції Лапласа, при значенні знаходимо . Тоді

У цьому випадку можна вважати, що з ймовірністю 0,95 страховій компанії гарантується прибуток

.

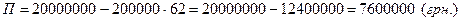Задача 5.1.3

Обчислити ймовірність появи події А від 50 до 70 раз в 95 випробуваннях, якщо ймовірність появи події у кожному випробуванні однакова і дорівнює 0,7.

Задача 5.1.4

Обчислити ймовірність появи події А від 60 до 65 рази в 75 випробуваннях, якщо ймовірність появи події у кожному випробуванні однакова і дорівнює 0,8.

Задача 5.1.5

Ймовірність появи події дорівнює 0,7 у кожному з 2100 незалежних випробувань. Знайти ймовірність появи події: а) не менше 1470 раз; б) не менше 1470 і не більше 1500 раз; в) не більше 1469 раз.

Задача 5.1.6

Банк надає кредит населенню і має 1000 клієнтів. Кожному з клієнтів надається кредит 50000 грн. при умові повернення 110% від цієї суми. Ймовірність неповернення кредиту кожним з клієнтів у середньому складає 0,01. Який прибуток гарантується банку з ймовірністю 0,9?

Поиск по сайту: