Розділ 2.4. Теорема додавання ймовірностей сумісних подій

Означення: Дві події називаються сумісними, якщо поява однієї з них не виключає появи іншої в одному й тому ж випробуванні.

Наприклад, подія “поява трьох очок при киданні грального кубика” і подія “поява непарного числа очок при киданні грального кубика” є сумісними.

Теорема: Ймовірність появи однієї з двох сумісних подій дорівнює сумі ймовірностей цих подій без ймовірності їх сумісної появи

. (2.7)

Доведення

Оскільки події А і В – сумісні, тоді подія А+В відбудеться, якщо відбудеться одна з трьох несумісних подій: .

.

Подія А відбудеться, якщо відбудеться одна з подій . За теоремою додавання:

Аналогічно:

Звідси:

.

При використанні одержаної формули треба мати на увазі, що події А і В можуть бути як залежними, так і незалежними, тому формула (2.7) набуде вигляду

для незалежних подій: ; (2.8)

для залежних подій: 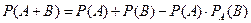. (2.9)

Наприклад:

Ймовірність одержання сертифікату якості для першого і другого виду виробів відповідно дорівнює =0,7 і =0,8. Знайти ймовірність одержання сертифікату якості хоча б одним виробом підприємства.

Рішення

Подія А – перший вироб одержить сертифікат якості.

Подія В – другий вироб одержить сертифікат якості.

Події А і В незалежні (одержання сертифікату якості першим виробом не залежить від одержання сертифікату другим).

Подія А+В – хоча б один вироб підприємства одержав сертифікат якості, тобто або перший (А), або другий (В), або обидва вироби (АВ), тоді за формулою (2.7)

= 0,7+0,8 - 0,7·0,8=0,94.

Поиск по сайту: