 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задачі до розділу 15.3
 Задача 15.3.1
Задача 15.3.1
За двома незалежними вибірками обсягів  і
і  , вилучених з нормальних генеральних сукупностей Х і У, знайдено виправлені вибіркові дисперсії
, вилучених з нормальних генеральних сукупностей Х і У, знайдено виправлені вибіркові дисперсії  і
і  . При рівні значущості
. При рівні значущості  перевірити нульову гіпотезу
перевірити нульову гіпотезу 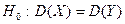 при конкуруючій гіпотезі
при конкуруючій гіпотезі  .
.
 Задача 15.3.2
Задача 15.3.2
За двома незалежними вибірками обсягів  і
і  , вилучених з нормальних генеральних сукупностей Х і У, знайдено виправлені вибіркові дисперсії
, вилучених з нормальних генеральних сукупностей Х і У, знайдено виправлені вибіркові дисперсії  і
і  . При рівні значущості
. При рівні значущості 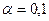 перевірити нульову гіпотезу
перевірити нульову гіпотезу 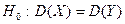 при конкуруючій гіпотезі
при конкуруючій гіпотезі  .
.
 Задача 15.3.3
Задача 15.3.3
Двома методами проведено вимірювання однакової фізичної величини. Одержано наступні результати
| Х | 9,2 | 10,8 | 9,7 | 8,8 | 10,2 | 9,9 | У | 10,6 | 10,2 | 9,8 | 10,8 |
Чи можна вважати, що обидва метода забезпечують однакову точність вимірювань, якщо прийняти рівень значущості 0,05? Припускається, що результати вимірювань розподілені нормально і вибірки є незалежними.
Розділ 15.4. Перевірка гіпотези про нормальний розподіл генеральної сукупності. (Критерій згоди  -Пірсона)
-Пірсона)
Як видно з попереднього розділу, гіпотеза про рівність дисперсій перевірялась при умові, що розподіл генеральних сукупностей був нормальним. Більшість гіпотез про параметри генеральної сукупності ґрунтується на твердженні про її нормальний розподіл. Якщо закон розподілу невідомий, то існують підстави, що він має певний вид (А), тоді перевіряють нульову гіпотезу
 : генеральна сукупність розподілена за законом А. Перевірка цієї гіпотези виконується за тим самим алгоритмом, що і перевірка гіпотез про параметри генеральної сукупності, тобто за допомогою випадкової величини – критерія згоди.
: генеральна сукупність розподілена за законом А. Перевірка цієї гіпотези виконується за тим самим алгоритмом, що і перевірка гіпотез про параметри генеральної сукупності, тобто за допомогою випадкової величини – критерія згоди.
 Означення: Критерієм згоди називається критерій перевірки гіпотези про можливий закон невідомого розподілу.
Означення: Критерієм згоди називається критерій перевірки гіпотези про можливий закон невідомого розподілу.
Існує декілька критеріїв згоди:  -Пірсона, Колмогорова, Смирнова і т.п.
-Пірсона, Колмогорова, Смирнова і т.п.
Розглянемо найбільш поширений у світовій практиці – критерій  -Пірсона, який є універсальним, тому його можна застосовувати до розподілів будь-якого виду.
-Пірсона, який є універсальним, тому його можна застосовувати до розподілів будь-якого виду.
Порівняємо емпіричні (спостережувальні) і теоретичні (обчислені у припущенні нормального розподілу) частоти, які звичайно будуть відрізнятися. Відмінність емпіричних і теоретичних частот пояснюється або малою кількістю спостережень та способом їх групування, або тим, що теоретичні частоти обраховані виходячи з невірного припущення про вид розподілу генеральної сукупності. Критерій  -Пірсона дає відповідь на всі ці питання. Як і всі інші критерії він не доводить справедливість гіпотези, а лише встановлює за прийнятим рівнем значущості її згоду або незгоду з даними спостережень.
-Пірсона дає відповідь на всі ці питання. Як і всі інші критерії він не доводить справедливість гіпотези, а лише встановлює за прийнятим рівнем значущості її згоду або незгоду з даними спостережень.
Нехай відомо
| Варіанти | 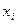
| 
| 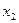
| ... | 
|
| Емпіричні частоти | 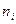
| 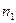
| 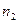
| ... | 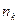
|
| Теоретичні частоти | 
| 
| 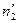
| ... | 
|
При рівні значущості  необхідно перевірити гіпотезу
необхідно перевірити гіпотезу  : генеральна сукупність має нормальний розподіл. За критерій перевірки нульової гіпотези приймаємо випадкову величину
: генеральна сукупність має нормальний розподіл. За критерій перевірки нульової гіпотези приймаємо випадкову величину
 . (15.3)
. (15.3)
Зрозуміло, що чим менше відрізняються емпіричні та теоретичні частоти, тим менша величина критерія (15.3) і тому він характеризує близькість емпіричного і теоретичного розподілу. Доведено, що при  закон розподілу випадкової величини, який задається формулою (15.3) незалежно від того, якому закону розподілу підлягає генеральна сукупність, прямує до розподілу
закон розподілу випадкової величини, який задається формулою (15.3) незалежно від того, якому закону розподілу підлягає генеральна сукупність, прямує до розподілу  з
з  степенями свободи. Тому випадкова величина (15.3) позначається через
степенями свободи. Тому випадкова величина (15.3) позначається через  , а сам критерій називається критерієм згоди „хі-квадрат”.
, а сам критерій називається критерієм згоди „хі-квадрат”.
Число степеней вільності знаходять із формули
 , (15.4)
, (15.4)
де 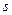 - число груп (частинних інтервалів) вибірки;
- число груп (частинних інтервалів) вибірки; 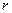 - число параметрів розподілу, який перевіряється за даними вибірки.
- число параметрів розподілу, який перевіряється за даними вибірки.
Наприклад, якщо мова йде про нормальний розподіл, то він задається диференціальною функцією 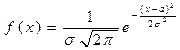 . Як видно з виду диференційної функції, нормальний розподіл задається двома параметрами (математичне сподівання і середнє квадратичне відхилення), тому
. Як видно з виду диференційної функції, нормальний розподіл задається двома параметрами (математичне сподівання і середнє квадратичне відхилення), тому  і число степенем свободи для нормального закону розподілу приймає значення
і число степенем свободи для нормального закону розподілу приймає значення
 . (15.5)
. (15.5)
Оскільки односторонній критерій більш жорстко перевіряє нульову гіпотезу, то візьмемо правосторонню критичну область, тоді
 (15.6)
(15.6)
Сформулюємо правило перевірки нульової гіпотези про вид розподілу генеральної сукупності.
 Методика перевірки гіпотези про нормальний розподіл генеральної сукупності
Методика перевірки гіпотези про нормальний розподіл генеральної сукупності
Для того, щоб при заданому рівні значущості  перевірити нульову гіпотезу
перевірити нульову гіпотезу  : генеральна сукупність має нормальний розподіл, потрібно спочатку обчислити теоретичні частоти, а потім спостережувальне значення критерія
: генеральна сукупність має нормальний розподіл, потрібно спочатку обчислити теоретичні частоти, а потім спостережувальне значення критерія  і за таблицею критичних точок розподілу
і за таблицею критичних точок розподілу  , за заданим рівнем значущості
, за заданим рівнем значущості  і числом степеней свободи
і числом степеней свободи  , знайти критичну точку
, знайти критичну точку  . Якщо
. Якщо 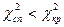 , тоді немає підстав відкидати нульову гіпотезу. Якщо
, тоді немає підстав відкидати нульову гіпотезу. Якщо 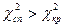 , тоді нульову гіпотезу відкидають.
, тоді нульову гіпотезу відкидають.
Треба зауважити, що при перевірці гіпотези про вид закону розподілу генеральної сукупності необхідно виконання декількох умов: обсяг вибірки повинен бути достатньо великим, кожний інтервал повинен вміщувати не менше 5-8 варіант, інтервали з меншою кількістю варіант потрібно об’єднувати, склавши їх частоти.
 Приклад:
Приклад:
При рівні значущості  перевірити гіпотезу про нормальний розподіл генеральної сукупності, якщо відомі емпіричні і теоретичні частоти
перевірити гіпотезу про нормальний розподіл генеральної сукупності, якщо відомі емпіричні і теоретичні частоти
| ||||||

|
Рішення
Результати розрахунків занесемо до таблиці
| № п/п | 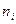
| 
| 
| ( )2 )2
| 
|
| 5,33 | |||||
| -2 | 0,22 | ||||
| -7 | 1,40 | ||||
| -7 | 0,94 | ||||
| 0,80 | |||||
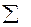
| 40,69 |
За таблицею критичних точок розподілу  , за заданим рівнем значущості
, за заданим рівнем значущості  і числом степеней свободи
і числом степеней свободи  , знайти критичну точку
, знайти критичну точку  . Оскільки
. Оскільки  , тобто
, тобто 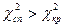 , тоді нульову гіпотезу відкидають.
, тоді нульову гіпотезу відкидають.
Поиск по сайту: