АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Рішення. Обсяг генеральної сукупності , тоді за формулою (12.2) знайдемо середню арифметичну

Читайте также:
  1. А. Рішення на застосування одного з перших трьох режимів радіаційного захисту
  2. Б. Рішення на застосування четвертого або п'ятого режимів радіаційного захисту
  3. Вирішення алгебричних рівнянь графічним методом за допомогою Simulink
  4. Вирішення диференційних рівнянь символічній формі
  5. Вирішення систем алгебричних рівнянь у символічній формі
  6. Вирішення систем диференційних рівнянь у символічній формі
  7. ВКАЗІВКИ ДО ВИРІШЕННЯ ЗАДАЧІ.
  8. ДЛЯ РІШЕННЯ ДЕЯКИХ ЗАДАЧ СТАТИСТИКИ
  9. Збори як форма прийняття колективного рішення
  10. Збори як форма прийняття колективного рішення. Нарада. Дискусія
  11. Зовнішні стіни з дрібнорозмірних елементів – конструктивні рішення; методи забезпечення необхідного опору теплопередачі.
  12. Інтернет–технології та їх використання для вирішення аналітичних задач на підприємстві

 

Обсяг генеральної сукупності , тоді за формулою (12.2) знайдемо середню арифметичну

 

 

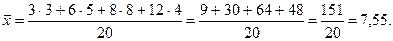
За формулою (12.4) знайдемо дисперсію

 

 

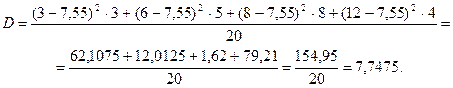
Як видно з означення, дисперсія характеризує відхилення від середньої у квадратних одиницях, що при розв’язанні задач змістовного характеру є незручним, тому вводять ще одну числову характеристику, яка характеризує розсіювання – середнє квадратичне відхилення.

Означення: Середнім квадратичним відхиленням називається корінь квадратний із дисперсії

 

(12.5)

 

 

Розділ 12.3. Формула для обчислення дисперсії. Властивості дисперсії

Як видно з попереднього розділу, обчислення дисперсії за означенням є досить громіздким, тому існує більш простий спосіб її обчислення.

Теорема: Дисперсія дорівнює середньому квадратів значень ознаки мінус квадрат загальної середньої.

 

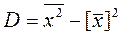. (12.6)

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)