АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Нормальний розподіл (розподіл Гауса)

Читайте также:
  1. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  2. V. Для дискретної випадкової величини Х, заданої рядом розподілу, знайти:
  3. Біноміальний закон розподілу
  4. Випадкові величини та їх розподіл
  5. Випадкові змінні х та у стохастично залежні, якщо зміна однієї з них викликає зміну розподілу другої (умовний розподіл однієї з них залежить від значень другої).
  6. Властивості емпіричної функції розподілу
  7. Властивості функції розподілу
  8. Геометричний закон розподілу
  9. Геометричний закон розподілу 1 страница
  10. Геометричний закон розподілу 2 страница
  11. Геометричний закон розподілу 3 страница
  12. Геометричний закон розподілу 4 страница

Означення: Нормальним називається розподіл ймовірностей неперервної випадкової величини, який описується диференціальною функцією.

. (10.11)

 

Як видно з запису диференціальної функції, нормальний розподіл визначається двома параметрами: математичним сподіванням 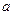і середнім квадратичним відхиленням .

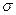Означення: Нормальний розподіл з параметрами і називається нормованим, його щільність (диференціальна функція) дорівнює

(10.12)

 

Графік диференціальної функції нормального розподілу для різних значень 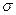наведено на рисунку 10.1. Крива на малюнку носить назву кривої Гауса.

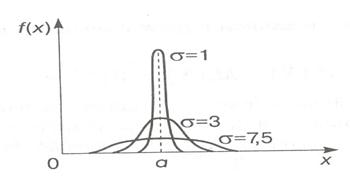
Рис.10.1. Графік диференціальної функції нормального розподілу

 

Інтегральна функція нормального розподілу згідно формули (8.7) заняття 8 буде мати вигляд

. (10.13)

 

Оскільки ця функція є парною, то невизначений інтеграл від неї є непарною функцією і тому, замість інтегральної функції (13) можна використати функцію Лапласа.

 

(10.14)

 

Ймовірність попадання в заданий інтервал нормальної випадкової


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)