 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задачі до розділу 7.2
 Задача 7.2.1
Задача 7.2.1
Знайти дисперсію та середнє квадратичне відхилення кількості очок, що випадають при киданні кубика.
Рішення
Перелічимо всі можливі значення дискретної випадкової величини Х – кількості очок, що випадають при киданні кубика Х: {1, 2, 3, 4, 5, 6}. Складемо закон розподілу ймовірностей дискретної випадкової величини Х.. Ймовірності випадання будь якої з шести можливих варіантів кількості очок однакові

| X | ||||||
| P | 
| 
| 
| 
| 
| 
|
Знайдемо математичне сподівання дискретної випадкової величини Х:

Знайдемо дисперсію дискретної випадкової величини Х двома способами: за означенням (І спосіб) і за теоремою (ІІ спосіб).
І спосіб
За формулою (7.1) знайдемо дисперсію щодобового продажу товару, для цього враховуючи, що М(Х)=3,5, складемо таблицю розподілу
| [Х-М(Х)]2 | (1-3,5)2 | (2-3,5)2 | (3-3,5)2 | (4-3,5)2 | (5-3,5)2 | (6-3,5)2 |
| P | 
| 
| 
| 
| 
| 
|

ІІ спосіб
Для застосування формули (7.3) складемо таблицю розподілу
| X2 | ||||||
| P | 
| 
| 
| 
| 
| 
|
 .
.
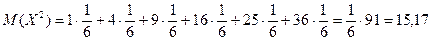
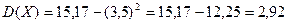 .
.
 Задача 7.2.2
Задача 7.2.2
Знайти двома способами дисперсію та середнє квадратичне відхилення дискретної випадкової величини, яка задана законом розподілу:
а)
| Х | -4 | -1 | ||||
| Р | 0,1 | 0,2 | 0,1 | 0,3 | 0,1 | 0,2 |
б)
| Х | |||||
| Р | 0,1 | 0,2 | 0,1 | 0,3 | Р5 |
 Задача 7.2.3
Задача 7.2.3
Закони розподілу дискретних незалежних випадкових величин Х та У наведено відповідно у таблицях
| Х | -2 | |||
| Р | 0,1 | 0,3 | 0,4 | 0,2 |
| У | ||||
| Р | 0,2 | 0,2 | 0,4 | 0,2 |
Знайти дисперсію та середнє квадратичне відхилення дискретної випадкової величини 3 Х+2У.
 Задача 7.2.4
Задача 7.2.4
Скласти закон розподілу дискретної випадкової величини Х – числа випадання „герба” при п’яти киданнях монети, знайти математичне сподівання, дисперсію і середнє квадратичне відхилення.
Поиск по сайту: