АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Розділ 5.2. Формула Пуассона

Читайте также:
  1. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  2. Барометрическая формула
  3. Барометрическая формула. Распределение Больцмана.
  4. Визначити енергію вибуху балону. Формула (3)
  5. Висновки до 3 розділу
  6. ВІДЦЕНТРОВІ ПИЛЕОСАДНІІ СУСПЕНЗІЙНО- РОЗДІЛЬНІ АПАРАТИ (ЦИКЛОНИ)
  7. Внешний фотоэффект и его законы. Формула Эйнштейна для фотоэффекта.
  8. Вопрос 2 Формула апостериорной вероятности Байеса
  9. Вопрос 2 Формула апостериорной вероятности Байеса.
  10. Вопрос 2 Формула апостериорной вероятности Байеса.
  11. Вставка розриву сторінки або розділу
  12. Гранична теорема Пуассона

Нехай виконується п незалежних випробувань в кожному з яких ймовірність появи події А дорівнює р. Для визначення ймовірності появи події рівно k раз в цих випробуваннях використовують формулу Бернуллі. Якщо ж п велике, тоді для визначення ймовірності появи використовують локальну теорему Лапласа. Але ця формула непридатна, якщо ймовірність появи події мала (). В цих випадках використовують формулу Пуассона.

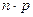Вважаємо, що добуток зберігає постійне значення, тобто . Для доведення формули Пуассона використаємо формулу Бернуллі

 

 

Оскільки , тоді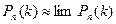

 

Значить формула Пуассона має вигляд:

 

. (5.3)

 

 

Приклад:

Завод відправив на базу 10000 якісних виробів. Ймовірність того, що на шляху до бази вироб втратить якість дорівнює 0,0001. Знайти ймовірність того, що на базу прийде 5 неякісних виробів.

 

Рішення.

 

За умовою задачі

 

Тоді

 

 

Пуассон Сімеон Дені (21.06.1781 – 25.04.1840 рр.) – французький механік, фізик і математик. Пуассон написав більше 300 праць, значна кількість яких відіграла значну роль у становленні сучасної науки. Він покращив способи застосування теорії ймовірностей взагалі і до питань статистики зокрема, довів теорему, яка стосується закону великих чисел (закон Пуассона), вперше ввівши термін „закон великих чисел”.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)