 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Розділ 16.4. Побудова рівняння квадратичної функції
 У випадку квадратичної функції
У випадку квадратичної функції  за формулою (16.1) знаходимо мінімум суми
за формулою (16.1) знаходимо мінімум суми  як функції трьох змінних a, b, c, при яких частинні похідні її повинні дорівнювати нулю
як функції трьох змінних a, b, c, при яких частинні похідні її повинні дорівнювати нулю
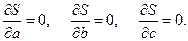
Знаходимо частинні похідні функції 

Прирівнюючи кожну з похідних до нуля отримуємо систему лінійних відносно a, b, c рівнянь
 (16.4)
(16.4)
 Приклад:
Приклад:
Статистичні дані витрат В підприємства і вкладень у модернізацію обладнання М наведено у вигляді таблиці.
| М | 3,5 | 4,1 | 4,5 | 4,2 | 5,5 | 5,7 | 6,3 | 7,5 | 8,0 | 8,0 |
| В | 13,0 | 8,5 | 6,5 | 5,0 | 3,3 | 2,9 | 2,9 | 5,2 | 7,0 | 9,1 |
Припускаючи, що між змінними В i М існує квадратична залежність, знайти емпіричну формулу 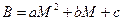 за методом найменших квадратів.
за методом найменших квадратів.
Рішення
Для спрощення обчислень позначимо витрати В через змінну у, а вкладення в модернізацію М через змінну х та складемо розрахункову таблицю.
| X (М) | Y (В) | x**2 | х**3 | х**4 | XY | х**2у | (Y) | (Y)-y |
| 3,5 | 12,25 | 42,875 | 150,0625 | 45,5 | 159,25 | 12,04065471 | -0,95935 | |
| 4,1 | 8,5 | 16,81 | 68,921 | 282,5761 | 34,85 | 142,885 | 8,074138338 | -0,42586 |
| 4,5 | 6,5 | 20,25 | 91,125 | 410,0625 | 29,25 | 131,625 | 6,016432497 | -0,48357 |
| 4,2 | 17,64 | 74,088 | 311,1696 | 88,2 | 7,515713997 | 2,515714 | ||
| 5,5 | 3,3 | 30,25 | 166,375 | 915,0625 | 18,15 | 99,825 | 2,925402328 | -0,3746 |
| 5,7 | 2,9 | 32,49 | 185,193 | 1055,6 | 16,53 | 94,221 | 2,65917934 | -0,24082 |
| 6,3 | 2,9 | 39,69 | 250,047 | 1575,296 | 18,27 | 115,101 | 2,564476465 | -0,33552 |
| 7,5 | 5,2 | 56,25 | 421,875 | 3164,063 | 292,5 | 5,542918124 | 0,342918 | |
| 8,0305421 | 1,030542 | |||||||
| 9,1 | 72,8 | 582,4 | 8,0305421 | -1,06946 | ||||
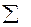 57,3 57,3
| 63,4 | 353,63 | 2324,499 | 16055,89 | 351,35 | 2154,007 | 63,4 | -1,3E-11 |
Використовуючи формулу (16.4) складемо систему для знаходження коефіцієнтів 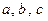

Знайдемо розв’язок системи рівнянь за формулами Крамера
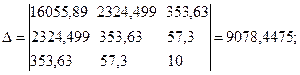




Тоді шукане рівняння набуде вигляду

За допомогою знайденого рівняння заповнимо два останні стовпці таблиці. Як видно із значення суми, рівняння знайдено правильно. На рисунку 3 представлено кореляційне поле, побудоване за статистичними даними, та рівняння параболи, побудоване за допомогою знайденого рівняння квадратичної лінії регресії.

Рис. 3
Розділ 16.5. Побудова рівняння гіперболічної функції
 Вирівнювання дослідних даних за гіперболою
Вирівнювання дослідних даних за гіперболою  здійснюється за допомогою заміни
здійснюється за допомогою заміни 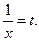 В такому разі в таблицю значень потрібно доповнити значеннями
В такому разі в таблицю значень потрібно доповнити значеннями 

| 
| 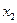
| … | 
| … | 
|
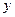
| 
| y2 | … | 
| … | 
|
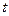
| 
| 
| … | 
| … | 
|
Після цього знаходиться мінімум функції  яка має такий самий вид, як й лінійна функція, тому відповідна система запишеться
яка має такий самий вид, як й лінійна функція, тому відповідна система запишеться
 (16.5)
(16.5)
Для отримання системи (16.5) складається відповідна обчислювальна таблиця відносно значень  з якої знаходять необхідні для системи суми. Після знаходження
з якої знаходять необхідні для системи суми. Після знаходження  отримуємо функцію
отримуємо функцію 
 Приклад:
Приклад:
Статистичні дані собівартості продукції С підприємства і обсягів виробництва продукції Q наведено у вигляді таблиці.
| Q | 1,5 | 1,6 | 2,6 | 3,4 | 3,8 | 6,1 | 8,2 | 9,1 | 11,3 | 11,9 |
| C | 8,1 | 6,8 | 4,2 | 2,6 | 2,3 | 1,5 | 1,3 | 1,1 | 0,8 | 1,2 |
Припускаючи, що між змінними C i Q існує гіперболічна залежність, знайти емпіричну формулу  за методом найменших квадратів.
за методом найменших квадратів.
Рішення
Для спрощення обчислень, позначимо собівартість виробленої продукції С через змінну у, а обсяги виробленої продукції Q через змінну х. Зробимо заміну  та складемо розрахункову таблицю.
та складемо розрахункову таблицю.
| X (Q) | Y (C) | t | t**2 | ty | (Y) | (Y)-Y |
| 1,5 | 8,1 | 0,666667 | 0,444444 | 5,4 | 7,523104 | -0,5769 |
| 1,6 | 6,8 | 0,625 | 0,390625 | 4,25 | 7,034387 | 0,234387 |
| 2,6 | 4,2 | 0,384615 | 0,147929 | 1,615385 | 4,21487 | 0,01487 |
| 3,4 | 2,6 | 0,294118 | 0,086505 | 0,764706 | 3,153404 | 0,553404 |
| 3,8 | 2,3 | 0,263158 | 0,069252 | 0,605263 | 2,790271 | 0,490271 |
| 6,1 | 1,5 | 0,163934 | 0,026874 | 0,245902 | 1,62646 | 0,12646 |
| 8,2 | 1,3 | 0,121951 | 0,014872 | 0,158537 | 1,134031 | -0,16597 |
| 9,1 | 1,1 | 0,10989 | 0,012076 | 0,120879 | 0,992563 | -0,10744 |
| 11,3 | 0,8 | 0,088496 | 0,007831 | 0,070796 | 0,741623 | -0,05838 |
| 11,9 | 1,2 | 0,084034 | 0,007062 | 0,10084 | 0,689288 | -0,51071 |
 59,5 59,5
| 29,9 | 2,801863 | 1,207471 | 13,33231 | 29,9 | 1,49E-14 |
Для знаходження параметрів рівняння гіперболи, складемо систему (16.5), яку розв’яжемо за формулами Крамера





Тоді шукане рівняння набуде вигляду

За допомогою знайденого рівняння заповнимо два останні стовпці таблиці. Як видно із значення суми, рівняння знайдено правильно. На рисунку 4 представлено кореляційне поле, побудоване за статистичними даними, та рівняння гіперболи, побудоване за допомогою знайденого рівняння вибіркової лінії регресії.

Рис.4
Розділ 16.6. Побудова рівняння показникової функції
 Вирівнювання дослідних даних за показниковою функцією
Вирівнювання дослідних даних за показниковою функцією  здійснюється за допомогою логарифмування
здійснюється за допомогою логарифмування 
 і подальшою заміною
і подальшою заміною 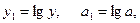
 Тоді отримаємо лінійну залежність
Тоді отримаємо лінійну залежність  параметри якої
параметри якої  знаходимо за розглянутим вище методом найменших квадратів.
знаходимо за розглянутим вище методом найменших квадратів.
 Приклад:
Приклад:
Статистичні дані витрат на зберігання продукції, що потребує охолодження В і температури зберігання Т наведено у вигляді таблиці.
| Т | -4,2 | -3,4 | -1,5 | -0,6 | 0,2 | 1,1 | 1,4 | 1,8 | 2,1 | 2,3 |
| В | 1,2 | 1,5 | 2,1 | 3,2 | 3,6 | 4,4 | 5,1 | 5,5 | 6,2 | 7,3 |
Припускаючи, що між змінними В i Т існує показникова залежність, знайти емпіричну формулу  за методом найменших квадратів.
за методом найменших квадратів.
Рішення
Для спрощення обчислень позначимо витрати на зберігання продукції В через змінну у, а температуру зберігання Т через змінну х. Зробимо заміну 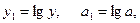
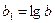 та складемо розрахункову таблицю.
та складемо розрахункову таблицю.
| X | Y | Y1=lgy | XУ1 | x**2 | (Y) | (Y)-y |
| -4,2 | 1,2 | 0,079181 | -0,33256 | 17,64 | 1,161586 | -0,03841 |
| -3,4 | 1,5 | 0,176091 | -0,59871 | 11,56 | 1,435501 | -0,0645 |
| -1,5 | 2,1 | 0,322219 | -0,48333 | 2,25 | 2,373502 | 0,273502 |
| -0,6 | 3,2 | 0,50515 | -0,30309 | 0,36 | 3,011866 | -0,18813 |
| 0,2 | 3,6 | 0,556303 | 0,111261 | 0,04 | 3,722097 | 0,122097 |
| 1,1 | 4,4 | 0,643453 | 0,707798 | 1,21 | 4,723171 | 0,323171 |
| 1,4 | 5,1 | 0,70757 | 0,990598 | 1,96 | 5,11347 | 0,01347 |
| 1,8 | 5,5 | 0,740363 | 1,332653 | 3,24 | 5,684492 | 0,184492 |
| 2,1 | 6,2 | 0,792392 | 1,664023 | 4,41 | 6,15423 | -0,04577 |
| 2,3 | 7,3 | 0,863323 | 1,985643 | 5,29 | 6,48876 | -0,81124 |
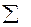 -0,8 -0,8
| 40,1 | 5,386044 | 5,074284 | 47,96 | 39,86867 | -0,23133 |
Аналогічно до методики побудови рівняння прямої, знайдемо коефіцієнти  і
і 





Повертаємося до заміни 
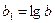 і знаходимо коефіцієнти
і знаходимо коефіцієнти 


Таким чином, шукане рівняння набуде вигляду
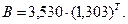
За допомогою знайденого рівняння заповнимо два останні стовпці таблиці. Як видно із значення суми, рівняння знайдено правильно. На рисунку 5 представлено кореляційне поле, побудоване за статистичними даними, та рівняння показникової функції, побудоване за допомогою знайденого рівняння вибіркової лінії регресії.

Рис. 5.
Розділ 16.7.Знаходження параметрів множинної лінійної залежності
 У моделюванні економічних процесів найбільшого розповсюдження набула залежність
У моделюванні економічних процесів найбільшого розповсюдження набула залежність
 . (16.6)
. (16.6)
Досить поширене використання цієї залежності пояснюється відносною простотою як її побудови, так і інтерпритації параметрів. Застосуємо до обчислення параметрів залежності (16.6) метод найменших квадратів.

Одержуємо систему

Після елементарних перетворень одержуємо систему рівнянь, з якоъ знаходимо параметри рывняння (10.6).
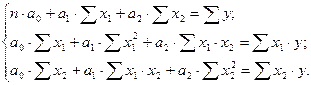
(16.7)
Аналогічним чином, можна побудувати трьохфакторне рівняння
 . (16.8)
. (16.8)
Після перетворень система (16.7) для визначення параметрів рівняння (16.8) набуде вигляду
 (16.9)
(16.9)
 Приклад: Розрахуємо параметри трьохфакторної лінійної функції, що встановлює залежність виробництва валової продукції у, млн. грн. підприємств від суми основних х1 і оборотних х2 виробничих фондів, млн. грн. і середньорічної чисельності працюючих х3, чол. Вихідні дані для побудови виробничої функції представлені у таблиці 1.
Приклад: Розрахуємо параметри трьохфакторної лінійної функції, що встановлює залежність виробництва валової продукції у, млн. грн. підприємств від суми основних х1 і оборотних х2 виробничих фондів, млн. грн. і середньорічної чисельності працюючих х3, чол. Вихідні дані для побудови виробничої функції представлені у таблиці 1.
Таблиця 1
Виробничі фонди, число працюючих і виробництво валової продукції підприємств
| х1 | х2 | х3 | у | 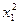
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| 4,1 | 16,81 | 41,0 | 12,3 | ||||||||||
| 5,6 | 31,36 | 67,2 | 28,0 | ||||||||||
| 3,1 | 9,61 | 21,7 | 6,2 | ||||||||||
| 6,4 | 40,96 | 83,2 | 38,4 | ||||||||||
| 8,6 | 73,96 | 154,8 | 60,2 | ||||||||||
| 5,5 | 30,25 | 60,5 | 27,5 | ||||||||||
| 11,0 | 121,00 | 253,0 | 110,0 | ||||||||||
| 7,9 | 62,41 | 126,4 | 63,2 | ||||||||||
| 3,8 | 14,44 | 26,6 | 11,4 | ||||||||||
| 8,5 | 72,25 | 144,5 | 59,5 | ||||||||||
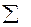
| |||||||||||||
| 64,5 | 473,05 | 978,9 | 416,7 |
Підставимо значення сум у систему (16.9) і одержимо систему з чотирьох рівнянь і чотирьох невідомих.

Знайдемо розв’язок системи (наприклад за методом Гаусса)

Звідси, лінійна функція, що відображає зв’язок виробництва вадової продукції від суми основних і оборотних фондів та числа працюючих, набуде вигляду
 .
.
Для перевірки точності обрахунків порівняємо емпіричні і теоретичні значення функції
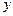
| 4,1 | 5,6 | 3,1 | 6,4 | 8,6 | 5,5 | 11,0 | 7,9 | 3,8 | 8,5 | 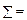 64,5 64,5
|

| 4,073 | 5,624 | 3,140 | 6,373 | 8,587 | 5,480 | 11,018 | 7,912 | 3,798 | 8,495 | 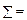 64,500 64,500
|
Як видно, сумарні значення емпіричних і теоретичних частот співпадають.
Розділ 17.1. Кореляційна таблиця
 При великій кількості спостережень одне й теж значення х може зустрічатися пх раз, одне й те ж значення у – пу раз, одна й таж пара чисел(х; у) може спостерігатися пху раз. Тому ці спостереження групуються, тобто підраховуються частоти пх, пу і пху. Всі згруповані дані записуються у вигляді таблиці, яку називають кореляційною.
При великій кількості спостережень одне й теж значення х може зустрічатися пх раз, одне й те ж значення у – пу раз, одна й таж пара чисел(х; у) може спостерігатися пху раз. Тому ці спостереження групуються, тобто підраховуються частоти пх, пу і пху. Всі згруповані дані записуються у вигляді таблиці, яку називають кореляційною.
 Приклад:
Приклад:
Кореляційну таблицю можна представити наступним чином
| У | Х | пу | |||
| -3 | |||||
| пх | п =25 |
У першому рядку таблиці вказано значення ознаки Х, що спостерігалася:
(5; 10; 15; 20), а у першому стовпці ознаки У: (-3; 3). На перетині рядків і стовпців знаходяться частоти пар значень ознак пху, що спостерігаються. Наприклад, частота 1 знаходиться на перетині значень ознак Х =5 і У = -3, тобто пара (5; -3) зустрічається 1 раз. В останній нижній клітині наведена кількість пар
(х; у).
Поиск по сайту: