Геометричний розподіл

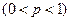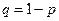Нехай проводяться незалежні випробування, в кожному з яких ймовірність появи події А дорівнює р , а . Випробування закінчуються як тільки з’явиться подія А. Таким чином, якщо подія А з’явиться у -му випробуванні, то у попередніх випробуваннях вона не з’явиться.

Позначимо через Х дискретну випадкову величину – числа випробувань, які треба провести до першої появи події А. Нехай в перших випробуваннях подія А не наступила, а в -му випробуванні з’явилася. Ймовірність цієї складної події за теоремою множення ймовірностей незалежних подій дорівнює

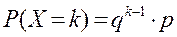, (10.5)

Як видно, формула (10.5) є геометричною прогресією з першим членом , знаменником

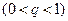
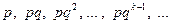
Тому розподіл, при якому ймовірність появи події А задається формулою (10.5), називається геометричною.

Приклад:

Робітник виготовляє вироб до першого бракованого. Ймовірність виготовлення бракованого виробу 0,2. Знайти ймовірність того, що бракований вироб буде третім.

Рішення

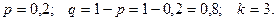
За формулою (10.5) знайдемо ймовірність влучення при третьому пострілі

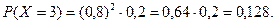
Поиск по сайту: