 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задачі до розділу 2.3
Задача 2.3.1
На складі зберігається продукція з трьох партій, відомо, що з I партії 90% продукції відповідає стандарту, з II партії – 80%, з III партії – 85%. З кожної партії обрано по одиниці продукції. Знайти ймовірність того, що всі три одиниці стандартні.
Рішення
Розглянемо події:
А – продукція I партії стандартна;
В – продукція II партії стандартна;
С – продукція III партії стандартна.
Обрання стандартної продукції з I, II, III партій є подіями незалежними, причому такими, що відбуваються одночасно. Тому застосуємо теорему множення ймовірностей незалежних подій.
Р(А) =0,9
Р(В) =0,8
Р(С) =0,85
Задача 2.3.2
Два біатлоністи стріляють по мішенях. Ймовірність влучення для першого біатлоніста 0.85, а для другого - 0.9. Знайти ймовірність того, що влучить у мішень тільки один біатлоніст.
Рішення
Подія А – влучить у мішень тільки один біатлоніст.
Подія А відбудеться у випадку: влучить в мішень тільки перший біатлоніст, а другий не влучить; або у випадку: влучить в мішень другий біатлоніст, а перший не влучить.
Позначимо події:
подія В –перший біатлоніст влучить у мішень;
подія С –другий біатлоніст влучить у мішень
і протилежні їм події:
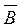- перший біатлоніст не влучить у мішень;
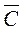- другий біатлоніст не влучить у мішень.
Тоді за допомогою теорем додавання й множення ймовірностей отримаємо:
Р(А)=Р(В) 
+ Р(С) 
,
де Р(В)= 0,85, Р(С)= 0,9, а протилежні їм події мають ймовірності
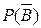= 1 - Р(В) = 1 – 0,85 = 0,15;
= 1 – Р(С) = 1 – 0,9 = 0,1.
Р(А) =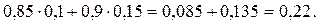 
Задача 2.3.3
Відділ технічного контролю перевіряє вироби на стандартність. Ймовірність того, що вироб стандартний 0.75. Знайти ймовірність того, що з трьох перевірених виробів тільки один стандартний.
Задача 2.3.4
Студент розшукує потрібне йому питання в трьох підручниках. Ймовірність того, що питання міститься в першому підручнику 0,4; в другому підручнику 0,7, а в третьому підручнику 0,75. Знайти ймовірність того, що питання міститься у всіх трьох підручниках.
Задача 2.3.5
Кинуто три гральних кубики. Знайти ймовірність того, що на верхніх гранях всіх кубиків випаде число 3.
Поиск по сайту: