Тоді за формулою (12.6) знайдемо дисперсію

1. Дати означення генеральної та вибіркової середньої.

2. У чому відмінність між генеральною та вибірковою середньою?

3. Записати формулу для обчислення середньої, якщо всі варіанти різні.

4. Записати формулу для обчислення середньої, якщо варіанти зустрічаються з певною частотою.

5. Що характеризує середня вибіркова?

6. Сформулювати властивості середньої.

7. Що характеризують дисперсія та середнє квадратичне відхилення?

8. Дати означення генеральної та вибіркової дисперсії.

9. Записати формулу для обчислення дисперсії, якщо всі варіанти різні.

10. Записати формулу для обчислення дисперсії, якщо варіанти зустрічаються з певною частотою.

11. Сформулювати теорему про обчислення дисперсії та пояснити значення складових у формулі обчислення дисперсії.

12. Сформулювати властивості дисперсії.

13. У чому відмінність між дисперсією і середнім квадратичним відхиленням?

Розділ 13.1. Коефіцієнт варіації

Означення: Коефіцієнт варіації дорівнює вираженому у відсотках відношенню середнього квадратичного відхилення до вибіркової середньої

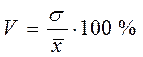. (13.1)

Коефіцієнт варіації служить для характеристики середньої, наскільки вона добре представляє статистичний ряд. Якщо варіаційні ряди мають однакові середні, тоді ряд з меншим коефіцієнтом варіації буде більш представницьким, тобто вибірка більш правильно представляє пропорції генеральної сукупності.

Якщо полігон варіаційного ряду не має значного скосу, тоді коефіцієнт варіації як правило менше 30%. Якщо коефіцієнт варіації більший за 100%, тоді можна зробити висновок, що спостереження є неоднорідними.

У задачах економічного спрямування за допомогою коефіцієнта варіації можна оцінити ризик від впровадження нової виробничої програми підприємства тощо.

Приклад:

Знайти коефіцієнт варіації для вибірки, яка задана статистичним розподілом

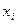
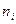
Знайти дисперсію.

Поиск по сайту: