Розділ 8.2. Диференціальна функція розподілу та її властивості

Нехай випадкова величина – неперервна, тоді функція розподілу F(x) теж неперервна. Нехай в околі точки х функція F(x) є диференційованою.

Означення: Диференціальною функцією розподілу f(x) називають першу похідну інтегральної функції F(x), тобто

. (8.5)

Властивість 1: Диференціальна функція є невід’ємною

.

Доведення

Ця властивість випливає із означення диференціальної функції як похідної від неспадної функції розподілу F(x). Геометрично це означає, що графік диференціальної функції розміщений або над віссю абсцис, або збігається з нею. Графік диференціальної функції називається кривою розподілу.

Властивість 2: Ймовірність того, що неперервна випадкова величина прийме значення з інтервалу 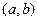дорівнює визначеному інтегралу від диференціальної функції, взятому в межах від а до b, тобто

(8.6)

Із наслідку 2 розділу 8.1 маємо

Якщо покласти у формулі (8.6) і застосувати теорему про середнє значення у визначному інтегралі, то її можна представити

Розділивши обидві частини в останній рівності на , отримаємо

Останнє відношення є середньою щільністю розподілу ймовірностей на проміжку . Якщо перейти до границі при то отримаємо

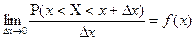. (8.7)

Формула (8.7) задає диференціальну функцію розподілу як щільність розподілу ймовірності неперервної випадкової величини в даній точці. У зв’язку з цим функцію f(x) називають диференціальною функцієюрозподілу або щільністю розподілу.

Приклад:

Дана диференціальна функція випадкової величини. Знайти ймовірність того, що за результатом випробування випадкова величина прийме значення з інтервалу (0,3; 1), якщо диференціальна функція дорівнює

Рішення

За формулою (8.6)

Властивість 3: Інтегральна функція розподілу може бути виражена через диференціальну

(8.8)

Доведення

Покладемо у формулі (8.8) маємо

Приклад:

Знайти інтегральну функцію за даною диференціальною функцією

Рішення

Якщо , тоді f(x)=0 F(x)=0. Якщо , тоді

Якщо ж , тоді

Властивість 4: Інтеграл у нескінченних межах від диференціальної функції дорівнює одиниці

(8.9)

Доведення

Цей вираз є ймовірністю події, яка полягає у тому, що випадкова величина прийме значення, яке належить , тобто є ймовірністю достовірної події, а ймовірність достовірної події дорівнює одиниці.

Геометрично це означає, що вся площа, обмежена віссю абсцис і кривою щільності розподілу, дорівнює одиниці. У цьому є аналогія щільності розподілу гістограми питомих відносних частот для статистичного ряду.

Приклад:

Диференціальна функція розподілу випадкової величини задана рівністю 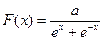, знайти параметр а.

Рішення

За формулою (8.9) одержуємо

тому що

Поиск по сайту: