Оцінка генеральної дисперсії по виправленій вибірковій

Означення: Статистичною оцінкою невідомого параметру теоретичного розподілу називається функція від величин, що спостерігаються.

Для того, щоб статистична оцінка давала гарне наближення параметрів, що оцінюються, вони повинні задовольняти певним вимогам, до яких відносяться: незміщеність, ефективність та спроможність.

Означення: Незміщеною називається статистична оцінка , математичне сподівання якої при довільному обсязі вибірки дорівнює параметру 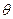, що оцінюється, тобто . Зміщеною називається оцінка, математичне сподівання якої не дорівнює параметру, що оцінюється.

Означення: Ефективною називається статистична оцінка, яка при заданому обсязі вибірки має найменшу можливу дисперсію.

При розгляді вибірок великого обсягу до статистичних оцінок застосовують вимогу спроможності.

Означення: Спроможною називається статистична оцінка, яка при прямує за ймовірністю до параметру, що оцінюється.

Наприклад, якщо дисперсія незміщеної оцінки при прямує до нуля, то така оцінка є спроможною.

Можна довести, що вибіркова середня є незміщена оцінка генеральної середньої, тобто

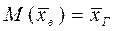. (14.4)

Якщо за оцінку генеральної дисперсії прийняти вибіркову дисперсію, то ця оцінка буде приводити до систематичних помилок, надаючи занижене значення генеральної дисперсії. Пояснюється це тим, що вибіркова дисперсія є зміщеною оцінкою генеральної дисперсії, іншими словами, математичне сподівання вибіркової дисперсії не дорівнює генеральній дисперсії, що оцінюється. Тому для оцінки генеральної дисперсії за вибірковою дисперсією застосовують поправку Бесселя

(14.5)

Легко виправити вибіркову дисперсію використовуючи поправку Бесселя, тоді виправлену дисперсію будемо позначати через

(14.6)

Як видно з формул виправленої 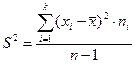і вибіркової 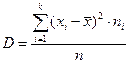дисперсій, вони відрізняються тільки знаменниками. Очевидно, що при досить великих обсягах вибірки вибіркова і виправлена дисперсії відрізняються мало. На практиці користуються виправленою дисперсією, якщо приблизно

Виправлене середнє квадратичне відхилення визначається за формулою

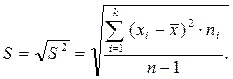(14.7)

Приклад:

Знайти виправлену дисперсію та виправлене середнє квадратичне відхилення за даними вибірки.

Рішення

Знайдемо середню вибіркову, враховуючи, що вона є незміщеною оцінкою

Оскільки обсяг вибірки менше 30, то знайдемо виправлену дисперсію та виправлене середнє квадратичне відхилення

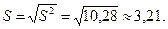
Бессель Фрідріх Вільгельм (22.07.1784 – 17.03.1846 рр.) – німецький астроном, член Берлінської академії наук. У 20 років обчислив орбіту комети Галлея. При обробці спостережень широко застосовував теорію ймовірностей і метод найменших квадратів. Його ім’ям названо клас трансцендентних функцій, а також одну з інтерполяційних формул, одне з лінійних диференціальних рівнянь другого порядку.

Поиск по сайту: