Задачі до розділу 1.2

Задача 1.2.1

Кидають два кубики. Знайти ймовірність того, що на верхніх гранях з’явиться кількість очок, сума яких буде менше п’яти.

Рішення

Подія А – на верхніх гранях з’являться числа, сума очок яких менше п’яти. Розглянемо всі можливі варіанти появ очок на першому і другому кубиках, виписавши їх:

1к. 2к. 1к. 2к. 1к. 2к. 1к. 2к. 1к. 2к. 1к. 2к.

1 1 2 1 3 1 4 1 5 1 6 1

1 2 2 2 3 2 4 2 5 2 6 2

1 3 2 3 3 3 4 3 5 3 6 3

1 4 2 4 3 4 4 4 5 4 6 4

1 5 2 5 3 5 4 5 5 5 6 5

1 6 2 6 3 6 4 6 5 6 6 6

На кожному з кубиків може випасти шість різних варіантів, а кількість кубиків два, тому всіх можливих випадків n = 6² = 36.

Розглянувши всі можливі варіанти оберемо сприятливі, їх буде m=6.

За класичним означенням ймовірності:

.

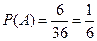Задача 1.2.2

Кинуто три монети. Знайти ймовірність того, що хоча б на двох монетах з’явиться „герб”.

Рішення

Розглянемо всі можливі варіанти, їх буде п = 2³ = 8 (на одній монеті можливі два випадки, всього монет три).

1 монета Г Г Г ч | ч | | ч| | ч | | ч|

2 монета Г Г ч Г | ч | | ч | | ч| | ч|

3 монета Г ч Г Г | ч | | ч| | ч| | ч|

Поняття „хоча б на двох монетах ” включає, що „герб” з’явиться або на двох з трьох, або на всіх трьох монетах. Тому кількість сприятливих подій буде m = 4. За класичним означенням ймовірності:

;

Задача 1.2.3

Кинуто чотири монети. Знайти ймовірність того, що на трьох з них з’явиться „герб”.

Задача 1.2.4

Кинуто два гральні кубика. Знайти ймовірність того, що сума очок, що випала, дорівнює восьми, а різниця чотирьом.

Задача 1.2.5

Кинуто три гральні кубика. Знайти ймовірність того, що на верхніх гранях з’являться тільки непарні числа очок.

Поиск по сайту: