 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Розділ 16.2. Метод найменших квадратів (загальні поняття)
 Будь-які випадкові величини можуть бути пов’язані функціональною залежністю, що буває досить рідко, або залежністю іншого роду, яку називають статистичною, або будуть незалежними.
Будь-які випадкові величини можуть бути пов’язані функціональною залежністю, що буває досить рідко, або залежністю іншого роду, яку називають статистичною, або будуть незалежними.
Означення: Статистичною називається залежність, при якій зміна однієї з величин веде до зміни розподілу іншої. Якщо зміна однієї з величин веде до зміни середнього значення іншої, тоді статистична залежність називається кореляційною.
При вивченні закономірностей в деяких дослідженнях інженерної справи, економіки, біології, медицини і т.п. приходиться аналітично описувати (у вигляді формули) зв'язок між двома змінними x та y. Для цього в процесі експериментів та спостережень вимірюють з можливою точністю окремі значення xi і відповідні їм значення yi (i=1,2,…,n), або отримують такі значення як статистичні дані. В результаті маємо таблицю значень.
| x | x1 | x2 | … | xi | … | xn |
| y | y1 | y2 | … | yi | … | yn |
Побудуємо у вибраній системі координат XOY точки Mi(xi, yi), координати яких відповідають даним таблиці.
Тепер виникає необхідність вибору відповідної функції y=f(x), яка б описувала зв'язок між x і y. Таку функцію називають емпіричною. В загальному випадку вибір емпіричної функції не є однозначним. Можна знайти лінію, яка б проходила через кожну з точок Mi, це може бути так званий інтерполяційний багаточлен (на рис. 1 це пунктирна лінія), порядок якого буде досить високим (на одиницю меншим, ніж кількість точок в таблиці). Крім того, дані таблиці можуть бути не досить точними внаслідок наявності похибок вимірювання, а також впливу інших факторів, які ми не завжди можемо врахувати. Тому дослідники віддають перевагу більш простим і зручнішим функціям, таким, як лінійна  , квадратична
, квадратична  , показникові
, показникові  , гіперболічна
, гіперболічна  і ін. Обрана функція повинна "найкращим" чином згладжувати експериментальні дані. В залежності від того, як вводиться поняття "найкраще згладжування" встановлюється той або інший метод вибору емпіричної залежності
і ін. Обрана функція повинна "найкращим" чином згладжувати експериментальні дані. В залежності від того, як вводиться поняття "найкраще згладжування" встановлюється той або інший метод вибору емпіричної залежності  (на рис. 1 – суцільна лінія). Найбільш часто застосовується так званий метод найменших квадратів, який дозволяє знаходити параметри обраної залежності
(на рис. 1 – суцільна лінія). Найбільш часто застосовується так званий метод найменших квадратів, який дозволяє знаходити параметри обраної залежності 
Позначимо через  відхилення емпіричної функції в точці
відхилення емпіричної функції в точці  від відповідного табличного (експериментального) значення
від відповідного табличного (експериментального) значення  . Зрозуміло (див. рис. 1), що
. Зрозуміло (див. рис. 1), що  можуть бути для одних
можуть бути для одних  додатніми, а для інших від'ємними. Тому їх сума може навіть дорівнювати нулю. Краще було б брати суму їх абсолютних величин
додатніми, а для інших від'ємними. Тому їх сума може навіть дорівнювати нулю. Краще було б брати суму їх абсолютних величин  але досліджувати суму, яка містить модулі величин складніше, ніж суму квадратів цих величин. Тому зупиняються на останньому
але досліджувати суму, яка містить модулі величин складніше, ніж суму квадратів цих величин. Тому зупиняються на останньому
 , (16.1)
, (16.1)
де  - теоретичне значення функції;
- теоретичне значення функції;  - статистичне значення функції.
- статистичне значення функції.
 |
Параметри функції  обирають так, щоб сума квадратів S приймала найменше значення.
обирають так, щоб сума квадратів S приймала найменше значення.
Розділ 16.3. Побудова рівняння лінійної функції
 Розглянемо випадок, коли
Розглянемо випадок, коли  є лінійною функцією з невідомими параметрами a i b. Тоді величина відхилення
є лінійною функцією з невідомими параметрами a i b. Тоді величина відхилення  , а сума їх квадратів
, а сума їх квадратів
 . (16.2)
. (16.2)
є функцією двох змінних a i b (xi, yi – числа з таблиці). За необхідною умовою існування екстремуму, функція S (a,b) приймає мінімальне значення при тих значеннях a i b, при яких частинні похідні по цих змінних дорівнюють нулю, тобто коли

Із формули (16.2) знаходимо 
Прирівнюючи до нуля частинні похідні, отримуємо систему рівнянь
 (16.3)
(16.3)
Система (16.3) називається нормальною системою методу найменших квадратів.
Розв'язуючи систему рівнянь (16.3), знаходять числа a i b, які підставляють у рівняння 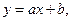 що і дає формулу шуканої залежності.
що і дає формулу шуканої залежності.
Метод найменших квадратів був запропонований німецьким математиком К. Гауссом.
 Приклад:
Приклад:
Статистичні дані чистого прибутку П підприємства і обсягів виробленої продукції  наведено у вигляді таблиці.
наведено у вигляді таблиці.
| П | -1,32 | -0,35 | 1,03 | 2,31 | 2,96 | 3,26 | 4,13 | 5,66 | 6,31 | 7,26 |

| 3,19 | 4,05 | 5,29 | 6,45 | 7,02 | 7,29 | 11,07 | 9,01 | 10,05 | 10,86 |
Припускаючи, що між змінними  і П існує лінійна залежність, знайти емпіричну формулу
і П існує лінійна залежність, знайти емпіричну формулу  за методом найменших квадратів.
за методом найменших квадратів.
Рішення
Складемо розрахункову таблицю.
| X | Y | x**2 | XY | (Y) | (Y)-y |
| -1,32 | 3,19 | 1,7424 | -4,2108 | 3,324191 | 0,134191 |
| -0,35 | 4,05 | 0,1225 | -1,4175 | 4,219735 | 0,169735 |
| 1,03 | 5,29 | 1,0609 | 5,4487 | 5,493809 | 0,203809 |
| 2,31 | 6,45 | 5,3361 | 14,8995 | 6,675558 | 0,225558 |
| 2,96 | 7,02 | 8,7616 | 20,7792 | 7,275665 | 0,255665 |
| 3,26 | 7,29 | 10,6276 | 23,7654 | 7,552638 | 0,262638 |
| 4,13 | 11,07 | 17,0569 | 45,7191 | 8,355858 | -2,71414 |
| 5,66 | 9,01 | 32,0356 | 50,9966 | 9,768417 | 0,758417 |
| 6,31 | 10,05 | 39,8161 | 63,4155 | 10,36852 | 0,318524 |
| 7,26 | 10,86 | 52,7076 | 78,8436 | 11,2456 | 0,385604 |
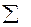 31,25 31,25
| 74,28 | 169,2673 | 298,2393 | 74,28 | -8,4E-15 |
За формулою (16.3) знайдемо коефіцієнти рівняння прямої лінії регресії

За формулами Крамера знайдемо розв’язок системи




Таким чином, рівняння прямої лінії регресії набуде вигляду
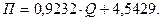
За допомогою знайденого рівняння заповнимо два останні стовпці таблиці. Як видно із значення суми, рівняння знайдено правильно. На рисунку 2 представлено кореляційне поле, побудоване за статистичними даними, та рівняння прямої, побудоване за допомогою знайденого рівняння прямої лінії регресії.

Рис.2
Поиск по сайту: