АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Розділ 3.1. Ймовірність появи хоча б однієї події

Читайте также:
  1. а) відношенню кількості елементарних подій, що сприяють події до кількості всіх
  2. В Мадриде появился отель из мусора
  3. В этот момент все искажения пропали, появилась картинка лагеря демонов, но почему-то вверх ногами. Под нашими вопросительными взглядами Сергей занервничал.
  4. Ва ціна однієї тонни – 3500 грн. Орендна плата визначена у 1700 грн.
  5. Випадкові змінні х та у стохастично залежні, якщо зміна однієї з них викликає зміну розподілу другої (умовний розподіл однієї з них залежить від значень другої).
  6. Випадкові події і величини, їх числові характеристики
  7. Випадкові події. Класифікація подій
  8. Висновки до 3 розділу
  9. Відкриття однієї фотографії
  10. ВІДЦЕНТРОВІ ПИЛЕОСАДНІІ СУСПЕНЗІЙНО- РОЗДІЛЬНІ АПАРАТИ (ЦИКЛОНИ)
  11. Вкажіть номер неправильної відповіді. Аварійні події на АЕС за збільшенням тяжкість класифікується по рівнях шкалою МАГАТЕ 1990г.
  12. Воєнно-політичні події в літку 1919 в березні 1920

Теорема: Ймовірність появи хоча б однієї з подій 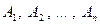, незалежних у сукупності, дорівнює різниці між одиницею і добутком ймовірностей протилежних подій .

 

. (3.1)

 

Доведення

 

Нехай подія А полягає в появі хоча б однієї з подій 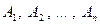. Подія А і подія (жодна з подій 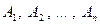не настала) протилежні, тому сума їх ймовірностей дорівнює одиниці.

.

Звідси

,

 

,

 

.

 

Наслідок: Якщо події 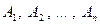мають однакову ймовірність, що дорівнює , тоді ймовірність появи хоча б однієї з цих подій визначається за формулою

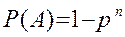. (3.2)

 

Наприклад:

 

1. Ймовірність виготовлення стандартної деталі на одному з трьох верстатів відповідно дорівнюють =0,8, = 0,85, = 0,9. Знайти ймовірність виготовлення хоча б однієї стандартної деталі при роботі на трьох верстатах (подія А).

Рішення

 

Знайдемо ймовірності протилежних подій (виготовлення нестандартних деталей на кожному з верстатів)

 

 

.

 

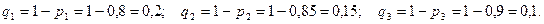
2. Ймовірність того, що подія відбудеться хоча б один раз в трьох незалежних в сукупності випробуваннях, дорівнює 0,964. Знайти ймовірність появи події в одному випробуванні, вважаючи, що ймовірність появи події в кожному випробуванні однакова.

Рішення

 

Використовуючи формулу (3.2), маємо

 

 


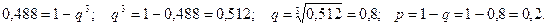
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)