АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Властивості середньої

Читайте также:
  1. А) Властивості бінарних відношень
  2. Атрибутивні ознаки і властивості культури
  3. Б) Основні властивості операцій над множинами
  4. БУДОВА Й ЕЛЕКТРИЧНІ ВЛАСТИВОСТІ НАПІВПРОВІДНИКІВ
  5. Вимоги до змісту загальної середньої освіти
  6. Властивості дисперсії
  7. Властивості диференціальної функції
  8. Властивості емпіричної функції
  9. Властивості емпіричної функції розподілу
  10. Властивості інтегральної функції
  11. Властивості ймовірностей подій
  12. Властивості ймовірності

 

Властивість 1: Якщо всі варіанти збільшити (зменшити) в одне й те ж число раз, то середня арифметична теж збільшиться (зменшиться) у стільки ж раз.

 

Доведення

 

Якщо кожну варіанту збільшити в раз, тоді за формулою (12.2) маємо

 

.

 

Властивість 2: Якщо всі варіанти збільшити (зменшити) на одне й те ж число, тоді середня арифметична збільшиться (зменшиться) на те ж саме число.

 

Доведення

 

Нехай кожна варіанта збільшилася на число С, тоді за формулою (12.2) маємо

 

 

Розділ 12.2. Генеральна і вибіркова дисперсії та середнє квадратичне відхилення

Для характеристики розсіювання значень кількісної ознаки Х навколо свого середнього значення вводять ще одну числову характеристику – дисперсію.

Означення: Генеральною дисперсією називається середнє арифметичне квадратів відхилення значень ознаки генеральної сукупності від її середнього значення. Вибірковою дисперсією називається середнє арифметичне квадратів відхилення значень ознаки вибіркової сукупності від її середнього значення.

Дисперсія визначається за формулою:

 

1) якщо всі варіанти різні

; (12.3)

 

2) якщо варіанти зустрічаються з певними частотами

 

. (12.4)

 

Приклад:

Сукупність задана таблицею розподілу

 

           
       

 

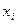
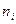
Знайти дисперсію.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.007 сек.)