АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Властивості диференціальної функції

Читайте также:
  1. III. Соціальна політика, її сутність і функції.
  2. А) Властивості бінарних відношень
  3. АБСТРАКТНІ КЛАСИ І ЧИСТІ ВІРТУАЛЬНІ ФУНКЦІЇ_________________________________________
  4. Автоматизоване робоче місце бухгалтера (АРМБ): призначення, функції та його рівні.
  5. Автоматизоване робоче місце бухгалтера (АРМБ): призначення, функції та його рівні.
  6. Алгоритм знаходження функції, оберненої до даної.
  7. Атрибутивні ознаки і властивості культури
  8. Б) Основні властивості операцій над множинами
  9. Банківська система. Банки, їх види та функції
  10. Банківська система. Банки, їх види та функції
  11. Біржова торгівля. Товарна та фондова біржа, їх функції та значення
  12. БУДОВА Й ЕЛЕКТРИЧНІ ВЛАСТИВОСТІ НАПІВПРОВІДНИКІВ

1. Диференціальна функція є невід’ємною .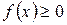

2. .

3. Ймовірність того, що неперервна випадкова величина прийме будь-яке значення з інтервалу 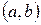дорівнює визначеному інтегралу від густини розподілу на цьому інтервалі

.

Зв’язок між інтегральною і диференціальною функціями

, .

5.3. Числові характеристики випадкових величин

 

Числовими характеристиками випадкової величини називаються характеристики, які у стислій формі виражають найбільш суттєві особливості розподілу.

Математичне сподівання (середнє значення).

Для дискретної випадкової величини –

.

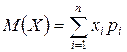Для неперервної випадкової величини –

.

Властивості математичного сподівання

1.

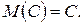
2.

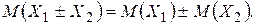
3. – для незалежних випадкових величин.

4.

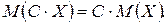
Дисперсія (міра розсіювання) –

,

– для дискретної випадкової величини,

– для неперервної випадкової величини.

Властивості дисперсії

1.

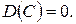
2. .

3. – для незалежних випадкових величин.

4. .

Середнє квадратичне відхилення –

.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.007 сек.)