АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Нехай отримано емпіричний варіаційний ряд ознаки

Читайте также:
  1. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  2. Акти застосування права: поняття, ознаки, види, структура
  3. Атрибутивні ознаки і властивості культури
  4. Держава як суб’єкт міжнародного приватного права. Імунітет держави: поняття, ознаки, види.
  5. ДЕРЖАВНІ ОРГАНИ: ЇХ ОЗНАКИ, ХАРАКТЕРИСТИКА І ВИДИ
  6. Дискретний варіаційний ряд часток
  7. Для знаходження середнього квадрата ознаки складемо таблицю
  8. ЗАГАЛЬНЕ ПОНЯТТЯ. СУТНІСТЬ І ОЗНАКИ ДЕРЖАВИ
  9. Інтервальний варіаційний ряд
  10. Інтервальний варіаційний ряд частот
  11. Кредитна система: суть, види, ознаки, складові
  12. Мова і культура мовлення в житті професійного комунікатора. Комунікативні ознаки культури мови

 

…
…

,

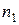
який вважають розподіленим за законом Пуассона. Для побудови цього закону слід виконати наступні дії:

§ обчислити і ;

§ перевірити їх на приблизну рівність;

§ взяти за параметр 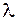величину .

 

Приклад. Було проведене спостереження викликів-замовлень за час на телефонному комутаторі:
Кількість викликів              
Кількість інтервалів              

.

Розглянута ознака (кількість викликів) може приймати лише послідовні цілочисельні значення. Вважаємо її розподіленою за законом Пуассона.

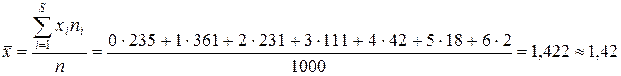
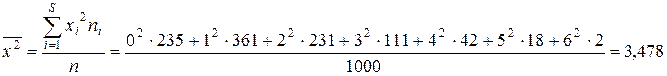
Середня приблизно дорівнює дисперсії, що дає підстави зробити висновок: для цього розподілу теоретичним буде закон Пуассона з параметром .

,

де


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)