 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теореми додавання ймовірностей
а) Ймовірність суми двох несумісних подій дорівнює сумі ймовірностей цих подій
 .
.
б) Ймовірність суми двох сумісних подій дорівнює сумі ймовірностей цих подій без ймовірності їх сумісної появи
 .
.
Зауваження. Варто мати на увазі, що коли події утворюють суму, то вони поєднуються союзом “чи” і навпаки.
в) Якщо події  утворюють повну групу, то сума їх ймовірностей дорівнює одиниці
утворюють повну групу, то сума їх ймовірностей дорівнює одиниці
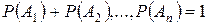 .
.
г) Принцип доцільності застосування протилежних подій: якщо протилежна подія розпадається на менше число варіантів, ніж пряма подія, то має сенс при обчисленні ймовірності перейти до протилежної події
 .
.
д) Виходячи з того, що сума подій полягає в появі хоча б одного з подій – складових, має сенс користатися іншою формулою:
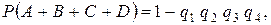
де 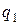 – ймовірність непояви
– ймовірність непояви  , тобто
, тобто  ,
,
 – ймовірність непояви
– ймовірність непояви  , тобто
, тобто  ,
,
 – ймовірність непояви
– ймовірність непояви  , тобто
, тобто  ,
,
 –ймовірність непояви
–ймовірність непояви 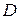 , тобто
, тобто  .
.
Поиск по сайту: